Page 6 - m5-secuencia03

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Matemáticas V. Secuencia didáctica para la unidad 3 Autor: Dr. José Manuel Becerra Espinosa

Recuérdese que la pendiente se define como el “cambio vertical” dividido por el “cambio horizontal” entre
dos puntos en una recta, o en otras palabras, la razón de la altitud − con respecto a la distancia
2
1
horizontal − entre dos puntos cualesquiera de la recta.
1
2

Entonces, dados dos puntos ( , ) y ( , ) en una recta, la pendiente está dada por:
2
1
2
1
1
2

− 1
2
=
− 1
2

Concluyendo, la pendiente permite determinar si una función es lineal ya que tiene como propiedad que
las diferencias entre los valores de la variable (dependiente) son constantes para iguales diferencias de
la variable (independiente).

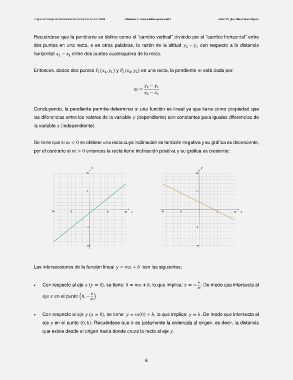
Se tiene que si < 0 se obtiene una recta cuya inclinación es también negativa y su gráfica es decreciente,

por el contrario si > 0 entonces la recta tiene inclinación positiva y su gráfica es creciente:

Las intersecciones de la función lineal = + son las siguientes:

 Con respecto al eje ( = 0), se tiene: 0 = + , lo que implica: = − . De modo que intersecta al

eje en el punto (0, − )

 Con respecto al eje ( = 0), se tiene: = (0) + , lo que implica: = . De modo que intersecta al
eje en el punto (0, ). Recuérdese que es justamente la ordenada al origen, es decir, la distancia

que existe desde el origen hasta donde cruza la recta al eje .

6