Page 8 - m4-secuencia04

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Matemáticas IV. Secuencia didáctica para la unidad 4 Autor: Dr. José Manuel Becerra Espinosa

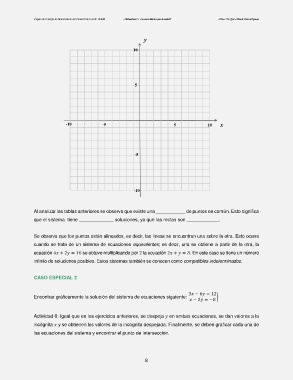
Al analizar las tablas anteriores se observa que existe una ___________ de puntos en común. Esto significa
que el sistema tiene _____________ soluciones, ya que las rectas son ____________.

Se observa que los puntos están alineados, es decir, las líneas se encuentran una sobre la otra. Esto ocurre
cuando se trata de un sistema de ecuaciones equivalentes; es decir, una se obtiene a partir de la otra, la
ecuación 4 + 2 = 16 se obtuvo multiplicando por 2 la ecuación 2 + = 8. En este caso se tiene un número
infinito de soluciones posibles. Estos sistemas también se conocen como compatibles indeterminados.

CASO ESPECIAL 2

3 − 6 = 12
Encontrar gráficamente la solución del sistema de ecuaciones siguiente: }
− 2 = −8

Actividad 6: Igual que en los ejercicios anteriores, se despeja en ambas ecuaciones, se dan valores a la
incógnita y se obtienen los valores de la incógnita despejada. Finalmente, se deben graficar cada una de
las ecuaciones del sistema y encontrar el punto de intersección.

8