PLANTEAMIENTO

Se expone forma de efectuar la suma algebraica de número complejos.

DEFINICIÓN DE NÚMERO COMPLEJO

Se denomina número complejo a toda una expresión de la forma donde son números reales e es la unidad imaginaria. El primer término del binomio es la parte real del número complejo y la segunda es su parte imaginaria.

En términos generales, el conjunto de los números complejos en forma binómica puede expresarse de la siguiente forma:

Ejemplos de números complejos:

FORMAS BINÓMICA Y VECTORIAL DE UN NÚMERO COMPLEJO

Los números complejos pueden representarse gráficamente trazando dos ejes perpendiculares. El eje de abscisas representa la parte real del número complejo y sobre el eje de ordenadas la parte imaginaria Por lo tanto, el número complejo  queda representado por el punto del plano.

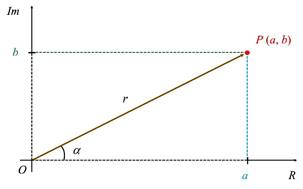
A la manera de representar un número complejo como se denomina forma vectorial.

SUMA ALGEBRAICA DE NÚMEROS COMPLEJOS

Sean y dos números complejos, entonces se define como:

Esto significa que se suman respectivamente las partes reales y las imaginarias. Esta operación sólo se puede efectuar en forma binómica y vectorial.

Ejemplos.

Sumar los siguientes números complejos:

1) y

Solución.

2) y

Solución.

Sean y dos números complejos, entonces se define como:

Para obtener la resta de dos números complejos se restan respectivamente las partes reales y las imaginarias. Al igual que la suma, la resta sólo se puede efectuar en forma binómica y vectorial.

Ejemplos.

Restar los siguientes números complejos:

1) y

Solución.

2) y

Solución.

CONCLUSIÓN

La suma de dos números complejos es otro número complejo cuya parte real es la suma de las partes reales y cuya parte imaginaria que es la suma de las partes imaginarias. La diferencia de dos números complejos es otro número complejo tal que su parte real es la diferencia de las partes reales y la parte imaginaria es la diferencia de las partes imaginarias.

PROPUESTA DE TRABAJO

1. Mover el punto azul y observar que representa al número complejo

2. Mover el punto verde y observar que representa al número complejo

3. Ver cómo se modifica la resultante de los vectores en color rojo que representa a

4. Comprobar los resultados de los ejemplos para la suma.

5. Notar que la resta en los números complejos es una suma con los sustraendos negativos.

6. Comprobar los resultados de los ejemplos para la resta considerando los sustraendos negativos, es decir, y respectivamente.

7. Concluir que la suma y resta algebraica de números complejos sólo se puede realizar en forma binómica o vectorial.

8. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.