PLANTEAMIENTO

Se expone forma de efectuar la potenciación de números complejos.

POTENCIA DE NÚMEROS IMAGINARIOS

Las potencias de superiores a uno se pueden reducir de la siguiente manera:

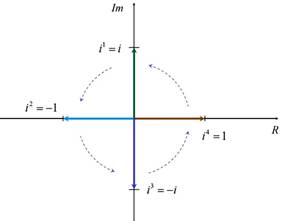
Si se graficaran los resultados anteriores se observa que las potencias inician en y que cada vez que se multiplica por el resultado gira 90° a la izquierda hasta que llega nuevamente a donde empieza un nuevo ciclo.

POTENCIA DE NÚMEROS COMPLEJOS

De acuerdo con el teorema de De Moivre, para encontrar la potencia enésima de un número complejo de la forma basta con elevar el módulo a esa potencia y el argumento multiplicarlo por Esto es:

Ejemplos.

1)

2)

CONCLUSIÓN

Para obtener la potencia enésima de un número complejo expresado en forma binómica se multiplica por sí mismo veces, sin embargo, en la práctica no se ocupa por la gran cantidad de operaciones que deben efectuarse. Conviene hacerlo en forma polar aplicando la expresión:

PROPUESTA DE TRABAJO

1. Mover el punto morado para fijar el módulo del número complejo

2. Mover el punto amarillo para fijar el argumento del número complejo

3. Mover el punto negro para establecer la potencia deseada.

4. Ver que el resultado de la potencia es el punto de color rojo.

5. Comprobar los resultados de los ejemplos.

6. Concluir que la potenciación conviene hacerla en forma polar y que por su similitud se obtienen fácilmente también en forma trigonométrica y cis.

7. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.