PLANTEAMIENTO

Se expone el concepto de número complejo, cómo se puede expresar y cómo convertir de forma binómica a forma polar.

DEFINICIÓN DE NÚMERO COMPLEJO

Se denomina número complejo a toda una expresión de la forma donde son números reales e es la unidad imaginaria. El primer término del binomio es la parte real del número complejo y la segunda es su parte imaginaria.

En términos generales, el conjunto de los números complejos en forma binómica puede expresarse de la siguiente forma:

Ejemplos de números complejos:

FORMAS BINÓMICA Y VECTORIAL DE UN NÚMERO COMPLEJO

Los números complejos pueden representarse gráficamente trazando dos ejes perpendiculares. El eje de abscisas representa la parte real del número complejo y sobre el eje de ordenadas la parte imaginaria Por lo tanto, el número complejo  queda representado por el punto del plano.

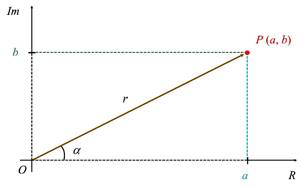
A la manera de representar un número complejo como se denomina forma vectorial.

FORMAS TRIGONOMÉTRICA, CIS Y POLAR DE UN NÚMERO COMPLEJO Y SU CONVERSIÓN DE LA FORMA BINÓMICA

De la figura anterior se aprecia que se forma un triángulo rectángulo, por lo tanto, aplicando el teorema de Pitágoras y considerando el módulo positivo, se tiene:

Por su parte, la tangente del ángulo está dada por:

El número se llama módulo y argumento del número complejo  Si se obtiene el argumento principal. 

La expresión  se llama forma trigonométrica del número complejo 

Si se le abrevia como el número complejo se expresa en su forma cis, esto es:

Para fines aún más prácticos, un número complejo puede expresarse en su forma polar o de Steinmetz como:

Hay que tener cuidado con la ubicación de los números en el plano a fin de no cometer errores con los signos. La siguiente tabla condensa los ajustes que deben aplicarse cuando no se tiene una calculadora que efectúe las conversiones de manera automática:

Signo	Cuadrante	Agregar al argumento:
+,+	I	0°
-,+	II	180°
-,-	III	180°
+,-	IV	0°

Ejemplo.

Convertir el número a su forma vectorial, trigonométrica y polar.

Solución.

En forma vectorial es:

como está en el primer cuadrante, el argumento no necesita ajuste.

de modo que:

CONCLUSIÓN

Existen varias formas de expresar un número complejo. Las dos más importantes son la binómica y la polar. Se puede convertir un número de la forma a la forma usando las expresiones y

PROPUESTA DE TRABAJO

1. Observar que en el plano, el eje horizontal corresponde la parte real y el eje vertical corresponde a la parte imaginaria.

2. Mover el deslizador azul, que representa la parte real del número complejo y ver cómo se modifica el módulo y el ángulo.

3. Mover el deslizador amarillo, que representa la parte imaginaria del número complejo y ver cómo se modifica el módulo y el ángulo.

4. Mover ambos deslizadores hasta ubicar el número y ver cuál es su forma polar.

5. Comprobar que es el mismo resultado que el obtenido en el ejemplo.

6. Modificar ambos deslizadores para ubicar diversos números complejos, obtener su respectiva forma polar y comprobar los resultados aplicando las fórmulas.

7. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.