PLANTEAMIENTO
Se explica el concepto de homotecia y se exponen sus propiedades.
HOMOTECIA
La semejanza se puede
expresar como una composición de rotaciones, traslaciones, reflexiones y
homotecias.
La homotecia es una transformación geométrica plana, en la cual los
puntos relacionados o transformados se denominan homotéticos, y cumplen las siguientes
condiciones:
–
Los puntos homotéticos están alineados con un
tercero fijo llamado centro de la homotecia ![]()
–
La relación entre los segmentos definidos por
este centro y los puntos transformado y original es una constante denominada
razón de la homotecia ![]()

PROPIEDADES DE LA
HOMOTECIA
Dos figuras homotéticas
guardan relación de semejanza.
El centro de la homotecia
es invariante, y las rectas que pasan por el centro de la homotecia también lo
son, aunque no lo son por puntos (los puntos no son dobles).
En
una homotecia pueden darse los siguientes casos, considerando el triángulo
amarillo ![]() como el original:
como el original:
–
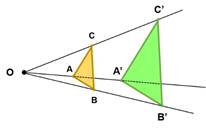
Si ![]() el tamaño de la figura transformada es mayor
que el de la original:
el tamaño de la figura transformada es mayor
que el de la original:
–
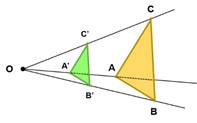
Si ![]() el tamaño de la figura transformada es menor
que el de la original:
el tamaño de la figura transformada es menor
que el de la original:
–
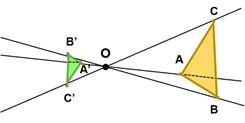
Si ![]() el tamaño de la figura transformada es menor
que el de la original:
el tamaño de la figura transformada es menor
que el de la original:
–
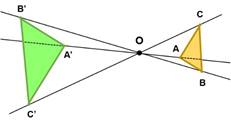
Si ![]() el tamaño de la figura transformada es mayor
que el de la original:
el tamaño de la figura transformada es mayor
que el de la original:
Nótese que cuando la
razón de homotecia ![]() ,
la figura semejante queda girada
respecto a la original.
,
la figura semejante queda girada
respecto a la original.
En una homotecia se
cumple:
–
El único punto invariante en una homotecia es
el centro de homotecia.
–
Las rectas que pasan por el centro de homotecia
son rectas invariantes.
–
Las rectas que contienen segmentos homólogos
son paralelas, y la razón de dichos segmentos coincide con la razón de
homotecia.
Si se aplica la
definición de homotecia a la figura:
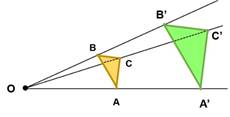
se tiene:
![]()
Los triángulos ![]() y
y ![]() son semejantes, ya que tienen un ángulo en
común y tienen los lados proporcionales.
son semejantes, ya que tienen un ángulo en
común y tienen los lados proporcionales.
Así pues, se cumplirá
que la razón entre los segmentos ![]() y
y ![]() es:
es:
![]()
–
Una homotecia conserva el sentido de las
figuras.
–
Una homotecia de razón ![]() transforma cada punto en sí mismo. Esta
homotecia recibe el nombre de identidad (las dos figuras coinciden).
transforma cada punto en sí mismo. Esta
homotecia recibe el nombre de identidad (las dos figuras coinciden).
–
Si la razón de una homotecia es ![]() se trata de una simetría central (que es una
rotación de
se trata de una simetría central (que es una
rotación de ![]() ).
).
PROPUESTA
DE TRABAJO
1.
Notar que los dos triángulos son semejantes.
2.
Mover el deslizador ![]() en el intervalo
en el intervalo ![]() y analizar el comportamiento del triángulo morado.
y analizar el comportamiento del triángulo morado.
3.
Ubicar el deslizador en ![]() y ver lo que le sucede al triángulo morado.
y ver lo que le sucede al triángulo morado.
4.
Mover el deslizador ![]() en el intervalo
en el intervalo ![]() y analizar el comportamiento del triángulo morado.
y analizar el comportamiento del triángulo morado.
5.
Ubicar el deslizador en ![]() y ver lo que le sucede al triángulo morado.
y ver lo que le sucede al triángulo morado.
6.
Mover el deslizador ![]() en el intervalo
en el intervalo ![]() y ver el comportamiento del triángulo morado.
y ver el comportamiento del triángulo morado.
7.
Ubicar el deslizador en ![]() y ver lo que le sucede al triángulo morado.
y ver lo que le sucede al triángulo morado.
8.
Mover el deslizador ![]() en el intervalo
en el intervalo ![]() y analizar el comportamiento del triángulo morado.
y analizar el comportamiento del triángulo morado.
9.
Pulsar el icono que se sitúa arriba a la derecha para
regresar a la construcción inicial.