PLANTEAMIENTO

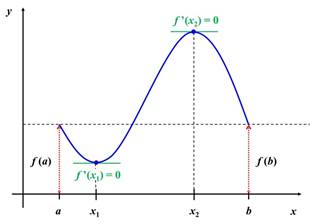
Se trata comprender el Teorema de Rolle: si una curva regular sale y llega a la misma altura, en algún punto tendrá tangente horizontal.

TESIS

Sea y = f (x) una función que cumple con las condiciones siguientes:

i. y = f (x) es continua en el intervalo cerrado [a,b]

ii. y = f (x) es derivable en el intervalo abierto (a,b)

iii. f (a)= f (b)

Por lo tanto existe, al menos un valor x que pertenece al intervalo (a,b), para el cual f '(x)=0

DEMOSTRACIÓN

Existen tres casos:

1. Si f (x) = 0 en el intervalo(a,b), entonces f '(x) = 0, para todo x , y así x puede ser cualquier valor en (a,b).

2. Si f (x) está por encima de f (a)=f (b) en algún punto del intervalo (a,b), entonces en un punto x₂ la función pasa de ser creciente a decreciente. Por definición, el punto donde ocurre eso es un máximo, por lo tanto f'(x₂)=0, en dicho intervalo.

3. Si f (x) está por debajo de f (a)= f (b) en algún punto del intervalo (a,b), entonces en un punto x₁ la función pasa de ser decreciente a creciente. Por definición, el punto donde ocurre eso es un mínimo, por lo tanto f'(x₁)=0, en dicho intervalo.

Puesto que toda función debe estar en uno de estos tres casos, el teorema queda demostrado.

CONCLUSIÓN

El teorema establece que por lo menos existe un punto de la gráfica de y = f (x), en el intervalo (a,b) en donde se tiene pendiente cero (tangente paralela al eje x) si sus extremos son de igual altura, ( f (a) = f (b)).

PROPUESTA DE TRABAJO

1. Comprobar que las alturas de f (a) y f (b) sean iguales moviendo el punto a.

2. Comprobar que el punto c, está en el intervalo (a,b).

3. La derivada en el punto representa la pendiente de la recta tangente de la curva.

4. Observar que se cumple que en algún punto del intervalo (a,b), la pendiente es cero.

5. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.