PLANTEAMIENTO
Se ilustran
geométricamente los conceptos de secante y tangente de una función.
SECANTE
Y TANGENTE DE UNA FUNCIÓN
Sea
una función 
y 
un punto del eje x. Si se toma un punto 
muy próximo a
(
es un número infinitamente pequeño), a medida
que se hace tender a cero, la recta secante (en color gris) que une los puntos: 
y 
, tiende a confundirse con la
tangente (en color verde) a
la curva en el punto .
Si 
es el ángulo que forma la secante con el eje
de las abscisas, y 
el ángulo que determina la tangente con ese
mismo eje, en el triángulo rectángulo de vértices:
, 
y
Se
cumple que:
Al
hacer tender a cero, y puesto que la secante tiende a
confundirse con un segmento de la tangente, es decir, si se observa la figura, al hacer que tienda a cero la recta gris se acerca a la recta verde
por lo que:
La 
tiende a
, es decir, a la pendiente de
la tangente a la curva en el punto 
. Esto se expresa
matemáticamente así:
Esta
expresión es la derivada de la
función en el punto y se denota como 
.
INTERPRETACIÓN
GRÁFICA
La tangente de un
ángulo es igual al cateto opuesto dividido entre el cateto adyacente, con lo
que se puede asociar la expresión:
con la tangente del
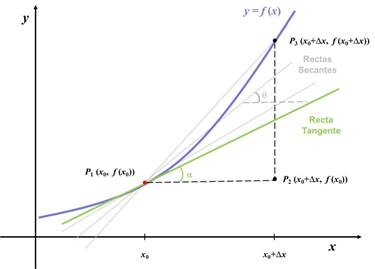
ángulo que forma la recta secante (recta gris desde P1 hasta el P3) con la horizontal.
Al incorporar el límite
cuando tiende a cero, el punto P3 se acerca al punto P1, de tal modo que en el
límite se encuentran infinitamente cerca, con lo que las rectas secantes (en
gris) dejan de ser secantes y se convierten en tangente (recta verde) a la
curva por el punto 
, ya que si es muy pequeño, los puntos y 
están infinitamente cerca.
Gráficamente esto es:
CONCLUSIÓN
La expresión de la
derivada representa al incremento vertical 
dividido entre el
incremento horizontal (lo que implica la inclinación de la función)
cuando el incremento horizontal es infinitamente pequeño (que
tiende a cero).
La derivada representa una
variación ya que indica como varía la
variable y según va lo hace la
variable x.
PROPUESTA
DE TRABAJO
1.
Mover el punto rojo P1 a donde se quiera obtener la derivada.
2.
Visualizar el valor de .
3.
Acercar lentamente y paulatinamente el punto verde P3 hacia el punto rojo P1 y comprobar que tienda
a cero.
4.
Verificar que el ángulo 
se
acerca a 
.
5.
Comprobar que cuando el punto verde P3 llega al punto rojo P1, la secante se convierte en tangente.
6.
Resaltar que el valor de la pendiente de la recta tangente es
el valor de la derivada de la función en el punto rojo P1.
7.
Pulsar el icono que se sitúa arriba a la derecha para
regresar a la construcción inicial.