PLANTEAMIENTO

Se muestra el concepto de recta tangente y de recta normal de una curva en un punto aplicando el concepto de derivada.

RECTA TANGENTE Y RECTA NORMAL DE UNA CURVA

Si una función posee una derivada en el punto , la curva tiene una tangente en cuya pendiente es: .

Se sabe que la ecuación de la recta que pasa por un punto y con una pendiente dada es: Por lo tanto, si se sustituye la pendiente por la derivada, la ecuación de la recta tangente en un punto de una curva es:

Una recta normal a una curva en uno de sus puntos es la recta que pasando por dicho punto es perpendicular a la recta tangente en él.

La condición de perpendicular entre dos rectas es:

La ecuación de la recta normal en el punto es:

Gráficamente esto es:

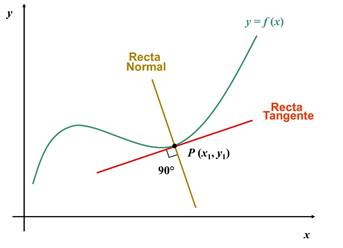
NÓTESE QUE:

Si tiene tangente horizontal a la curva. Si tiene tangente vertical a la curva.

PROPUESTA DE TRABAJO

1. Mover los coeficientes de la función cuadrática a través de los deslizadores para observar su comportamiento.

2. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.

3. Notar que la pendiente de la curva es la derivada de f (x) evaluada en el punto .

4. Visualizar que la recta en color verde es la recta tangente en el punto .

5. Activar la casilla para ver la ecuación de la recta tangente.

6. Notar que la pendiente de la curva es perpendicular a en el punto .

7. Observar que la recta en color morado es la recta normal en el punto y forma un ángulo recto con la recta tangente.

8. Activar la casilla para ver la ecuación de la recta normal.

9. Por medio de los deslizadores, establecer la función , ubicar el punto en y comprobar que por lo que tiene una tangente horizontal a la curva y que , lo que geométricamente implica que tiene una tangente vertical.