PLANTEAMIENTO

Se ilustra geométricamente lo que significa un punto crítico, así como el concepto de máximo y de mínimo de una función.

FUNCIÓN CRECIENTE

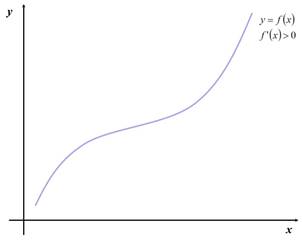
Una función f derivable, es estrictamente creciente en un punto a si, y sólo si .

Geométricamente significa que la pendiente de la recta tangente en dicho punto es positiva. Es creciente en un intervalo si todos los puntos cumplen con esta condición.

FUNCIÓN DECRECIENTE

Una función f derivable, es estrictamente decreciente en un punto a si, y sólo si .

Geométricamente significa que la pendiente de la recta tangente en dicho punto es negativa. Es decreciente en un intervalo si todos los puntos cumplen con esta condición.

PUNTO CRÍTICO DE UNA FUNCIÓN

Una función f derivable posee un punto crítico cuando su derivada es cero, es decir cuando tiene una recta tangente horizontal.

Las abscisas de los puntos críticos se obtienen derivando la función, igualando a cero y obteniendo sus raíces reales. Sus ordenadas se calculan sustituyendo las raíces en la función original.

MÍNIMO DE UNA FUNCIÓN

Si la función f pasa en un entorno del punto crítico de ser decreciente a creciente posee un mínimo.

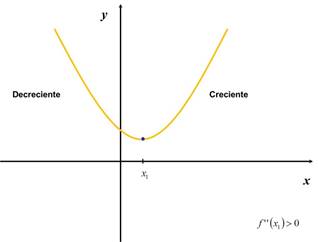
O bien, que si la segunda derivada de f en el punto crítico sea positiva.

MÁXIMO DE UNA FUNCIÓN

Si la función f pasa en un entorno del punto crítico de ser creciente a decreciente posee un máximo.

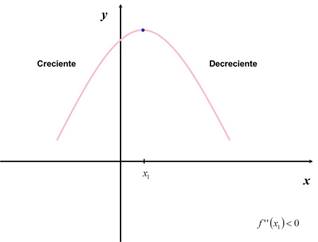
O bien, que la segunda derivada de f en el punto crítico sea negativa.

CONCLUSIÓN

La primera derivada de la función sirve para obtener los puntos críticos de una función. La segunda, es útil para conocer su naturaleza, ya sea máximo o mínimo.

PROPUESTA DE TRABAJO

1. Mover lentamente el punto verde y observar el comportamiento de la pendiente.

2. Notar que la pendiente es negativa antes de llegar al punto , que es cero en ese punto y después es positiva. Ese punto crítico es un mínimo.

3. Observar que la pendiente es positiva antes de llegar al punto , que es cero en ese punto y después es negativa. Ese punto crítico es un máximo.

4. Notar que la pendiente es negativa antes de llegar al punto , que es cero en ese punto y después es positiva. Ese punto crítico es un mínimo.

5. Mover los parámetros de la función hasta llegar a .

6. Repetir el proceso y concluir que ahora sólo se tienen dos puntos críticos.

7. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.