PLANTEAMIENTO
Se ilustra la variante
geométrica que existe entre el concepto de incremento y de diferencial.
INCREMENTO
Cuando la variable independiente x pasa de un valor inicial 
a un valor final 
, a la diferencia 
, representada por 
, se le llama incremento de la variable x, esto es:
De la misma manera, cuando la función 
pasa de un valor inicial 
a un valor final , a la diferencia 
, representada por 
, se le llama incremento de la función,
denotado por . Esto es:
Gráficamente esto es:
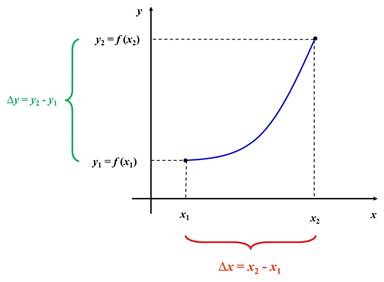
Ejemplo.
Obtener y de la función 
cuando x pasa de 1 a 1.4.
Solución:
DIFERENCIAL
Sea una función 
La diferencial de la
variable independiente se define como: 
La diferencial de la
variable dependiente se define como: 
La diferencial de la
variable x es por definición igual al incremento que
experimenta. Pero la diferencial de la variable y no es igual su
incremento:
La diferencial de y es el
resultado de multiplicar la derivada de la función por la diferencial de x.
VARIACIÓN ENTRE EL INCREMENTO Y LA DIFERENCIAL
Dado un punto P de abscisa x en la función , si se le da un incremento , se tendrá otro punto Q de abscisa 
Ahora, trazando la tangente a la curva en el
punto 
y desde 
se levanta una paralela al eje de ordenadas
hasta cortar a la curva y a la tangente, se aprecia claramente como la
diferencial 
y el incremento 
no son iguales.
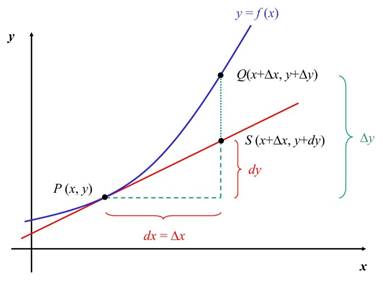
es lo que se
incrementa la recta tangente y es lo que se incrementa la función cuando se aumenta
x
en .
El
porcentaje de error en que se incurre por utilizar el incremento en lugar de la
diferencial está dado por:
Un error de
menos de 3 % es aceptado
como una buena aproximación.
Este
porcentaje depende plenamente del valor de , ya que
cuanto menor sea, mejor será la aproximación.
Ejemplo.
Obtener
, y el 
de la función 
cuando x pasa de:
a)
2 a 2.3
Solución:
error alto, por lo que no es
aceptable como aproximación.
b)
2 a 2.001
Solución:
error muy bajo, por lo que
es aceptable como muy buena aproximación.
CONCLUSIÓN
La recta tangente es la mejor aproximación lineal a la
función en el entorno del punto de tangencia. Si tiende a cero se puede sustituir por y el error en que se incurre es mínimo.
PROPUESTA
DE TRABAJO
1.
Observar que la recta roja representa a la tangente de la
función en café en el punto 
.
2.
Verificar que se genera un triángulo cuyo cateto adyacente es
y el
cateto opuesto es .
3.
Mover el punto y
comprobar que la diferencial de x es igual a su incremento: . Esto se muestra en color morado.
4.
Observar que es
la diferencia de ordenadas entre los puntos 
y . Esto se muestra en color rosa.
5.
Observar que es
la diferencia de ordenadas entre los puntos 
y . Esto se muestra en color azul.
6.
Mover lentamente el punto a la derecha y comprobar que la diferencial
de x y su incremento se comportan de manera
diferente. Su discrepancia aumenta.
7.
Mover lentamente el punto a la
izquierda hasta acercarlo al punto x1 y observar que la discrepancia entre la
diferencial de y y su incremento
cada vez es menor. Es decir que
cuando 
tiende a cero.
8.
Pulsar el icono que se sitúa arriba a la derecha para
regresar a la construcción inicial.