PLANTEAMIENTO

Se ilustra geométricamente el concepto de función definida por intervalos.

FUNCIÓN DEFINIDA POR INTERVALOS

Existen funciones que no pueden representarse mediante una única expresión. Por ejemplo, si se considera la función que le asigna a los números negativos el -1 y a los números positivos el 1, no se puede hallar ninguna expresión para dicha función. En estos casos se divide el dominio de la función en partes, de tal forma que para cada parte del dominio, se pueda encontrar una expresión que se ajuste a la función dada. Este tipo de funciones reciben el nombre de funciones definidas por intervalos.

En el caso anterior, el dominio quedaría divido en dos partes: los números negativos, para los cuales corresponde la expresión , y los números positivos, para los cuales corresponde la expresión . Se escribe:

Nótese como no está definida para el punto , por lo que su dominio es:

Sin embargo, hay funciones que existen para todo valor de x pero que no son continuas. Por ejemplo:

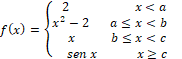
Se tienen tres puntos sobre el eje x que generan cuatro intervalos y depende de sus valores la continuidad de la función.

CONCLUSIÓN

Una función definida por intervalos (trozos o ramas) es aquella cuya expresión analítica contiene más de una fórmula, de modo que para distintos valores de la variable independiente x, se deben usar distintas fórmulas que permitan calcular la imagen y que les corresponde.

PROPUESTA DE TRABAJO

1. Mover el deslizador del punto a en rosa para ver el comportamiento de la función.

2. Desplazar el deslizador del punto b en azul para ver el comportamiento de la función.

3. Mover el deslizador del punto c en verde para ver el comportamiento de la función.

4. Ubicar los valores de a, b y c para que la función sea continua en .

5. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.