PLANTEAMIENTO
Se expone el comportamiento de la función de distribución normal.
DISTRIBUCIÓN NORMAL
Se dice que muchos
fenómenos se distribuyen normalmente. Esto significa que si uno toma al azar un
número suficientemente grande de casos y construye un polígono de frecuencias
con alguna variable continua, por ejemplo peso, talla, presión arterial o
temperatura, se obtendrá una curva de características particulares, llamada
distribución normal. Es la base del análisis estadístico, ya que en ella se
sustenta casi toda la inferencia estadística.
La función de densidad de probabilidad para la variable aleatoria continua
fue descubierta por Carl Gauss al estudiar el comportamiento de los procesos
aleatorios. Es ampliamente utilizada en estadística y teoría de las
probabilidades.
Esta función, también
conocida como distribución normal
tiene la forma de una campana, por este motivo también es conocida como la campana de Gauss. Sus características
son las siguientes:
•
Es una distribución simétrica.
•
Es asintótica, es decir sus extremos nunca
tocan el eje horizontal, cuyos valores tienden a infinito.
•
En el centro de la curva se encuentran la
media, la mediana y la moda.
•
El área total bajo la curva representa el 100%
de los casos.
•
Los elementos centrales del modelo son la media
y la varianza.
Esta distribución es un
modelo matemático que permite determinar probabilidades de ocurrencia para
distintos valores de la variable.
Esta función tiene un
comportamiento muy similar a la función 
, cuya tabulación y gráfica son las siguientes:
|
|
|
|
-2 |
0.018315 |
|
-1 |
0.367879 |
|
-0.8 |
0.527292 |
|
-0.6 |
0.697676 |
|
-0.4 |
0.852143 |
|
-0.2 |
0.960789 |
|
0 |
1 |
|
0.2 |
0.960789 |
|
0.4 |
0.852143 |
|
0.6 |
0.697676 |
|
0.8 |
0.527292 |
|
1 |
0.367879 |
|
2 |
0.018315 |
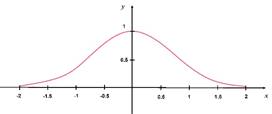
De acuerdo con lo anterior, se aprecian las siguientes características:
1. Su dominio es 
2. Es continua.
3. Su rango es 
4. 
5. Su derivada es: 
6. El máximo de la función se ubica en el punto 
La distribución normal
sirve para conocer la probabilidad de encontrar un valor de la variable que sea
igual o inferior a un cierto valor 
, conociendo
la media, la desviación estándar, y la varianza de un conjunto de datos en
sustituyéndolos en la función que describe el modelo. El cálculo resulta
bastante complejo pero, afortunadamente, existen tablas estandarizadas que
permiten eludir este procedimiento.
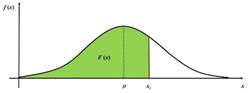
Su aplicación más
importante es que en la gráfica, el área sombreada corresponde a la probabilidad
de encontrar un valor de la variable que sea igual o inferior a un valor dado.
Esa probabilidad se determina usando una tabla estandarizada.
CONCLUSIÓN
La distribución normal es
la más frecuentemente utilizada y sus propiedades son el fundamento de los procedimientos
de inferencia importantes ya que la mayor parte de las variables aleatorias de
los fenómenos naturales presentan un comportamiento semejante al de esta
distribución, de ahí su nombre. En cursos de Estadística más avanzados, se verá
su utilidad.
PROPUESTA
DE TRABAJO
1.
Visualizar y comprobar que la distribución
normal presenta forma de campana.
2.
Mover el deslizador 
y analizar el comportamiento de la función.
3.
Mover el deslizador 
y analizar el comportamiento de la función.
4.
Mover los deslizadores 
y 
que en Probabilidad y Estadística sirven para
calcular porcentajes de que ocurra un evento.
5.
La curva normal es asintótica al eje de
abscisas. Por ello, cualquier valor
entre y es teóricamente posible. El área
total bajo la curva es, por tanto, igual a 
6.
Notar que esta función tiene un comportamiento
muy similar a la función
7.
Concluir que la distribución normal es una
distribución con forma de campana donde las desviaciones estándar sucesivas con
respecto a la media establecen valores de referencia para estimar el porcentaje
de observaciones de los datos.
8.
Pulsar el icono que se sitúa arriba a la derecha para
regresar a la construcción inicial.