PLANTEAMIENTO
Se ilustra
geométricamente el concepto de diferencial de una función.
DEFINICIÓN
DE DIFERENCIAL
Sea una función 
.
Se define como la diferencial
de la variable independiente a
:
Se define como la diferencial
de la variable dependiente a: 
Esto significa que la
diferencial de la variable x es por definición
igual al incremento que experimenta, sin embargo, la diferencial de la variable
y
no es igual su incremento:
INTERPRETACIÓN
GEOMÉTRICA DE LA DIFERENCIAL
Sea una función .
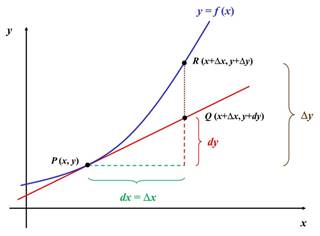
Dado un punto P de abscisa x,
si se le dota de un incremento 
, se tendrá otro punto Q de abscisa
. Ahora, si se traza la tangente a la curva en el punto 
, y desde 
se levanta
una paralela al eje de ordenadas hasta cortar a la curva y a la tangente, se
aprecia claramente como la diferencial 
y el
incremento 
no son
iguales.
PROPIEDADES
DE LA DIFERENCIAL
1) La diferencial de una función en un punto depende de dos variables: el
punto x elegido y el incremento que se ha tomado.
2) Al ser , la diferencial de una función en un punto es el incremento de la
ordenada de la tangente al aumentar en un punto de abscisa x.
3) Si se considera la función , se tiene
que:
, y pasando 
al primer miembro: 
. Por
lo tanto, se puede establecer que la derivada es un cociente de
diferenciales: 
.
4) Puesto que 
, de la noción de límite se deduce que cuando es infinitamente pequeño, el cociente 
es prácticamente igual a 
, y puesto que , es
prácticamente igual a 
, es decir,
que 
. Esta
propiedad permite sustituir por cuando es muy pequeño, con la seguridad de que el error cometido será mínimo.
CONCLUSIÓN
La diferencial es la variación que sufre la ordenada de la
recta tangente a la curva cuando la variable independiente x se
incrementa en . Por su
parte, el incremento es la variación que sufre la ordenada de la
curva cuando la variable independiente x se incrementa en .
PROPUESTA
DE TRABAJO
1.
Mover el punto rojo x2 y
visualizar la variación de .
2.
Observar como cambian y .
3.
Acercar lentamente y paulatinamente el punto rojo x2 hacia el punto azul x1 y comprobar que tienda
a cero.
4.
Verificar que el incremento se
acerca a la diferencial .
5.
Comprobar que cuando la recta secante en color rosa se convierte en
la tangente de color rojo.
6.
Resaltar que , y
que sólo cuando 
entonces .
7.
Pulsar el icono que se sitúa arriba a la derecha para
regresar a la construcción inicial.
8.
Mediante los deslizadores, modificar la función y repetir el
proceso de análisis.