PLANTEAMIENTO
Se ilustra
geométricamente cómo se comporta la derivada de la función secante.
DEFINICIÓN
La función secante es
de la forma ![]() .
.
Posee las siguientes
características:
·
El dominio de la función es: ![]()
·
El rango de la función es: ![]()
· Es periódica.
·
Posee un periodo de ![]()
· Es discontinua.
Su gráfica es:
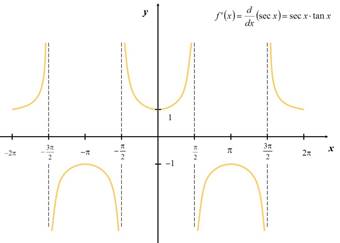
DERIVACIÓN
DE LA FUNCIÓN SECANTE
Sea la función ![]()
Aplicando la identidad
trigonométrica ![]() se tiene:
se tiene:
![]()
Derivando la función
como un cociente:
![]()
![]()
Así que:
![]()
Por lo tanto:
![]()
CONCLUSIÓN
La derivada de la función cotangente es
igual al producto de la función secante por la función tangente.
PROPUESTA
DE TRABAJO
1.
Mover el punto verde ![]() y
observar cómo se comporta la pendiente de la tangente de la función secante en
color gris.
y
observar cómo se comporta la pendiente de la tangente de la función secante en
color gris.
2.
Notar que la pendiente de la recta tangente es la ordenada de
la función derivada cuya abscisa es la misma que la del punto ![]() .
.
3.
Comprobar esto activando la casilla que activa el trazo.
4.
La gráfica en rojo representa la función ![]() .
.
5.
Pulsar el icono que se sitúa arriba a la derecha para
regresar a la construcción inicial.