PLANTEAMIENTO

Se ilustra geométricamente como se comporta la derivada de la función logarítmica.

DEFINICIÓN

Una función se llama logarítmica cuando es de la forma donde la base a es un número real positivo y distinto de uno.

Sea una función

En general, posee las siguientes características:

· El dominio de la función es:

· El rango de la función es:

· No cruza al eje y.

· Corta al eje x en el punto

· Pasa por el punto

· Es continua.

Se tienen dos casos:

1. Cuando la base a es mayor que uno siempre es creciente y lo es más, a medida que la base se acerca a uno.

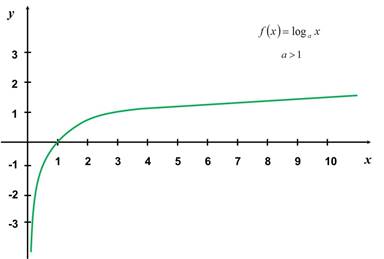
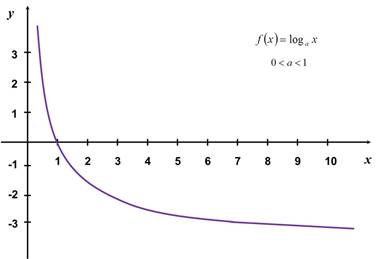
2. Cuando la base a es mayor que cero y menor que uno la función es decreciente y lo es más, a medida que su base se aproxima a cero.

DERIVACIÓN DE LA FUNCIÓN LOGARÍTMICA

Aplicando la regla de los cuatro pasos para obtener su derivada se tiene:

1^er Paso:

2^o Paso:

3^er Paso:

4^o Paso:

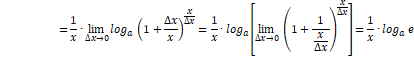
Por lo tanto:

CONCLUSIÓN

La derivada de un logaritmo en base a es igual a la derivada de la función dividida por la función por el logaritmo en base a del número e.

PROPUESTA DE TRABAJO

1. Modificar el deslizador hacia la derecha y observar como se comporta la función logarítmica.

2. Mover el deslizador hacia la izquierda hasta llegar y observar lo que le sucede a la función logarítmica.

3. Regresar el deslizador hacia la izquierda hasta llegar .

4. Modificar el deslizador hacia la derecha. Mover el punto rosa y observar como se comporta la pendiente de la tangente de la función logarítmica en color rosa.

5. Notar que la pendiente de la recta tangente es la ordenada de la función derivada cuya abscisa es la misma que la del punto .

6. Comprobar esto activando la casilla que activa el trazo.

7. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.

8. Repetir el proceso para diferentes valores de la base a y analizar el comportamiento de la función derivada.

9. Notar que si la base es el número e, entonces la derivada se convierte en: .