PLANTEAMIENTO

Se trata mostrar la representación gráfica del concepto de derivada de una función.

La derivada de una función f (x) en un punto x = a es el valor del límite, si existe, del cociente incremental cuando el incremento de la variable tiende a cero.

SECANTES Y TANGENTE DE UNA CURVA

Sea una función f (x) que cuyo punto Q se mueve de forma que se acerca a P, tal y como lo muestra la figura:

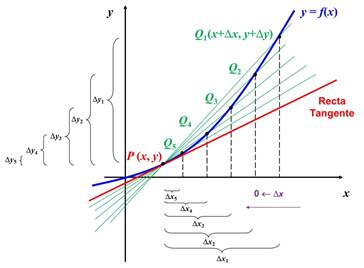
Una recta es secante a una curva cuando la corta en dos puntos distintos. En la figura se acrecían cinco secantes en color verde.

Es tangente a la curva cuando la toca en un sólo punto. En la figura es la recta en rojo.

Las pendientes de las rectas secantes sucesivas a la curva de la figura son los cocientes incrementales:

La pendiente de la recta tangente a la curva de la figura en un punto es cuando el punto Q se acerca a P. La derivada de la función se obtiene cuando los dos puntos están muy cercanos en la curva, es decir, cuando en el cociente incremental tiende a cero. Cuanto más cercanos sean los dos puntos que se unen por medio de la recta, las secantes se parecen más a una tangente a la curva. Matemáticamente es:

NÓTESE QUE:

a. El valor de la derivada de una función en un punto puede interpretase geométricamente, ya que se corresponde con pendiente de la recta tangente a la gráfica de la función en dicho punto.

b. La derivada de una función en un punto es un número real.

PROPUESTA DE TRABAJO

1. Identificar el cociente incremental entre los puntos x = 4 y x = 6.

2. Mover el punto hacia la derecha e identificar el cociente incremental y el valor de la pendiente de la secante entre x = 5 y x = 6.

3. Repetir el paso 2 entre x = 5.8 y x = 6.

4. Ubicar el valor del cociente incremental entre 5.999 y 6, o lo más aproximado que se pueda.

5. ¿Qué sucede con el cociente incremental en x = 6?

6. Explicar la relación que hay entre el cociente incremental y la recta tangente a la curva en el punto.

7. Concluir lo que representa gráficamente la derivada de una función en un punto.