PLANTEAMIENTO

Se ilustra geométricamente el concepto de límite de una función.

CONCEPTO DE LÍMITE

El límite de la función f (x) en el punto a, es el valor al que se acercan las imágenes (las y) cuando las x se acercan al valor a. Es decir el valor al que tienden las imágenes cuando las x tienden a a.

Se dice que la función f (x) tiene como límite el número L, cuando x tiende a a, si fijado un número real positivo ε, mayor que cero, existe un número positivo dependiente de , tal que, para todos los valores de x distintos de a que cumplen la condición:

0 < |x - a| < δ, se cumple que:

| f (x) - L| <ε

Se puede deducir de la definición, que para que exista el límite L de una función f (x) es necesario que se forme un entorno de L en f (x) siempre y cuando se pueda generar un entorno reducido de a en x.

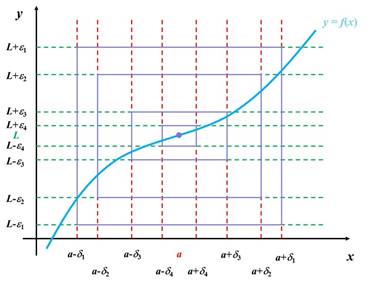
Dado que el entorno de L es: , el entorno reducido de a es: , donde y pueden se tan pequeñas como se desee, por lo que se pueden generar una infinidad de entornos cada vez más pequeños, siempre que . Esto puede interpretarse como la formación de rectángulos cada vez más pequeños que incluyan al punto (a, L).

Gráficamente esto es:

Existen funciones en las que a veces no es posible calcular directamente el límite en algún punto. Esto es debido a que estas funciones están definidas de diferente forma a la izquierda y a la derecha de ese punto. Para estudiar estos límites, se necesita recurrir a los límites laterales.

La condición necesaria y suficiente para que una función f (x) tenga límite en un punto de abscisa a es que tenga un límite lateral por la izquierda, tenga límite lateral por la derecha y ambos sean iguales. Si una función es convergente o tiene límite en un punto, éste debe ser único. Además, toda función que tiene límite en un punto está acotada en un entorno de ese punto.

Para calcular el límite de una función en un punto, no interesa lo que sucede en dicho punto sino a su alrededor.

LÍMITE POR LA IZQUIERDA

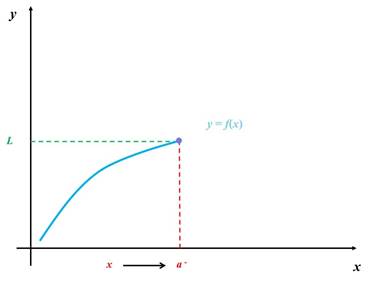
El límite de una función f (x) cuando x tiende hacia el punto a por la izquierda es L, si y sólo si:

Para todo > 0 existe > 0 tal que:

si x (a - , a), entonces |f (x) - L| < .

Gráficamente esto es:

LÍMITE POR LA DERECHA

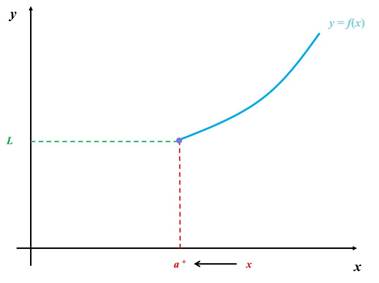
El límite de una función f (x) cuando x tiende hacia el punto a por la derecha es L, si y sólo si:

Para todo > 0 existe > 0 tal que:

si x (a, a+), entonces |f (x) - L| < .

Gráficamente esto es:

CONCLUSIÓN

El límite de una función en un punto si existe, es único. La inexistencia de un límite está condicionada por lo siguiente:

a) Si no existe alguno de los límites laterales, el límite no existe.

b) Si los límites laterales existen pero son diferentes, el límite no existe.

PROPUESTA DE TRABAJO

1. Mover el punto rosa a y fijarlo. Ese es el punto en donde se quiere obtener el límite de la función.

2. Mover el punto rojo x a la izquierda en dirección del punto verde para ver el comportamiento de límite lateral derecho L_d de la función.

3. Mover el punto rojo x a la derecha en dirección del punto verde para ver el comportamiento de límite lateral izquierdo L_i de la función.

4. Comprobar que los límites laterales son distintos cuando los puntos rojo y verde son iguales. Eso significa que la función es discontinua y el límite no existe.

5. Mover el punto a para hacer que el límite exista a través de la igualdad de los límites laterales.

6. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.