PLANTEAMIENTO
Se ilustra
geométricamente el concepto de función.
CONCEPTO
DE FUNCIÓN
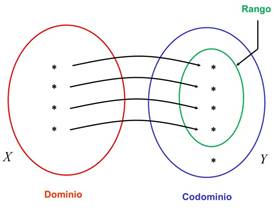
Una función matemática es la correspondencia o relación f de
los elementos de un conjunto X con los elementos de un
conjunto Y. Una función cumple con
la condición de existencia (todos los
elementos de X están relacionados con los elementos de Y) y con la condición de unicidad (cada elemento de X está relacionado con un
único elemento de Y).
En términos de variables,
una función es una correspondencia entre dos variables, de manera que a cada
valor de la primera le corresponde un único valor de la segunda (o ninguno) que
se le conoce como imagen.
A la función se le suele
designar por f y a la
imagen por f (x), siendo x la variable independiente.
La variable independiente es la que se fija
previamente.
La variable dependiente es la que se deduce de la
variable independiente.
Las funciones son como sistemas
a las que se les introduce un elemento x y devuelven otro valor y, que también se designa
por f (x).
DOMINIO,
IMAGEN Y RANGO DE UNA FUNCIÓN
El dominio de una función 
está
formado por aquellos valores reales de x
para los que se puede calcular la imagen f (x). Es el conjunto de elementos de x que hace posible que la función exista. Se puede
determinar de distintas formas dependiendo del tipo de función que se tenga.
Para determinarlo se debe
verificar donde la función no existe, y que en general, se toma en cuenta lo
siguiente:
1) No existe la división entre cero.
2) Las raíces negativas de índice par no pueden ser negativas.
El rango de una función 
está formado por aquellos valores reales de y que son imágenes del conjunto de elementos que
conforman el dominio de la función. Es decir, el conjunto de elementos de y que hace posible que la
función exista.
Para determinar el rango
de una función, se despeja x si es posible, se observa el comportamiento de y se hace un análisis
similar al que se hizo para determinar el dominio.
Ejemplo.
Obtener el dominio y
rango de las siguientes funciones:
1) 
Solución.
Se puede ver que si x toma el valor de 2, entonces se tiene una división por cero. Así que la
función existe para todos los valores de x
excepto en x = 2. Lo que matemáticamente se expresa
como:
Para obtener el rango, se
despeja la variable independiente y se analiza el comportamiento de y:
Se puede ver que si y toma el valor de 0, entonces se tiene
una división por cero. Así que x existe para todos los valores de y excepto en y = 0.
Lo que matemáticamente se expresa como:
2) 
Se puede ver que sólo si x toma valor mayores o iguales a 4, entonces la
función tiene sentido. Lo que matemáticamente se expresa como:
Para obtener el rango, se
analiza el comportamiento de y:
El resultado de una raíz
cuadrada siempre es positiva o cero. Así que x existe para todos los valores de y positivos o cero.
Lo que matemáticamente se expresa como:
PRUEBA
DE LA RECTA VERTICAL
Las funciones están bien
definidas si solamente se puede asignar un resultado a cada entrada. En otras
palabras, cada valor de x
(entrada) puede tener un solo valor de y
(resultado) directamente relacionado.
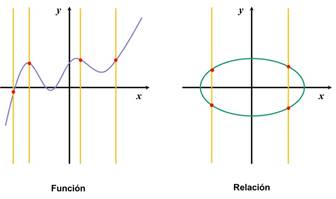
La prueba de la recta
vertical establece que un conjunto de puntos en el plano es la gráfica de una
función sí cualquier recta vertical intersecta la curva sólo en un punto.
CONCLUSIÓN
Una función f es
una relación entre un conjunto
dado X (llamado dominio) y otro conjunto de elementos Y (llamado codominio) de forma que a cada elemento x del dominio le corresponde un único elemento f (x) del
codominio. Al conjunto de imágenes se le conoce como rango.
PROPUESTA
DE TRABAJO
1.
Identificar que la columna A de la tabla representa los
valores del dominio de la función.
2.
Identificar que la columna B de la tabla representa los
valores de las imágenes de los valores del dominio y que cada valor se eleva al
cuadrado.
3.
Notar que la columna C se forman las parejas ordenadas de
algunos puntos de la función y que se representan en el plano.
4.
Advertir que estos puntos son algunos de la infinidad que
conforman la función 
, que puede verse en su totalidad al
activar la casilla.
5.
Ver que el dominio de la función es: 
6.
Notar que el rango de la función es: