PLANTEAMIENTO

Se ilustra geométricamente lo que significa la concavidad y convexidad de una función, así como el concepto de punto de inflexión.

CONCAVIDAD Y CONVEXIDAD

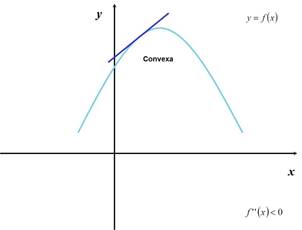
Una función es convexa si la gráfica de la función queda por encima de la recta tangente en cada punto.

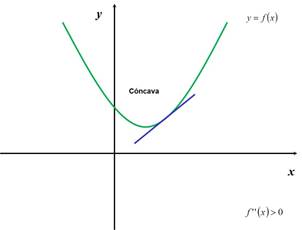
Una función es cóncava si la gráfica de la función queda por debajo de la recta tangente en cada punto.

El criterio de la segunda derivada para determinar la concavidad o convexidad es:

Si f es convexa entonces f '' < 0.

Si f es cóncava entonces f '' > 0.

PUNTO DE INFLEXIÓN

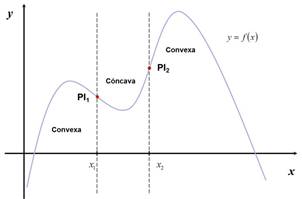
Un punto a es de inflexión si en dicho punto la función pasa de cóncava a convexa o viceversa. Es decir si f '' (a) = 0.

CONCLUSIÓN

Para calcular los intervalos de concavidad y convexidad de una función de forma práctica, generalmente:

1. Se obtiene la derivada segunda y se calculan sus raíces (si las hay), que son los puntos de inflexión.

2. Se forman intervalos abiertos con las raíces de la derivada segunda y los puntos de discontinuidad (si los hay).

3. Se toma un valor de cada intervalo, y se encuentra el signo que tiene en la derivada segunda con el siguiente criterio:

· Si f '' (x) > 0 es cóncava.

· Si f '' (x) < 0 es convexa.

4. Se escriben los intervalos.

PROPUESTA DE TRABAJO

1. Mover lentamente el punto verde y observar el comportamiento de la pendiente.

2. Identificar los puntos de inflexión PI₁ y PI₂.

3. Notar que la pendiente siempre está por encima de la función antes del punto PI₁. En ese intervalo la función es convexa.

4. Observar que la pendiente siempre está por debajo de la curva entre los puntos PI₁ y PI₂. En ese intervalo la función es cóncava.

5. Notar que la pendiente siempre está por encima de la función después del punto PI₂. En ese intervalo la función vuelve a ser convexa.

6. Mover los parámetros de la función hasta llegar a .

7. Repetir el proceso y concluir que ahora sólo se tiene un punto crítico.

8. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.