PLANTEAMIENTO
Se trata analizar el
comportamiento del área que se limita por la intersección entre dos curvas planas.
El área comprendida entre
dos funciones es igual al área de la función que está situada por encima menos
el área de la función que está situada por debajo.
PROCEDIMIENTO
Sea una región del plano
encerrada por una curva. El área de esa región puede calcularse mediante
integral definida. La expresión de esa integral depende de la forma en la que
esté expresada la curva.
El área limitada
entre una curva 
, el eje x y las rectas x
= a y x = b es:
El área limitada
entre la curva , la curva 
y considerando que a y b son las abscisas de los puntos de intersección viene dada
por:
EJEMPLOS
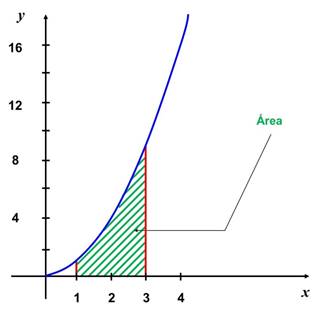
1) Curva 
, el eje x y por las
rectas x
= 1 y
x = 3.
Solución.
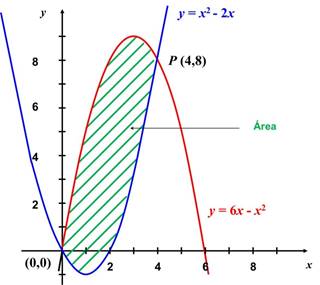
2) Hallar el área
comprendida entre las parábolas 
y 
.
Solución.
Igualando las
ecuaciones para obtener los puntos de intersección:
Factorizando:
los
puntos de intersección son: 
y 
.
Área pedida = Área bajo
la parábola 1 - Área bajo la parábola 2:
El applet de la derecha muestra el caso del área limitada entre una
parábola y una recta.
PROPUESTA
DE TRABAJO
1.
Mover los coeficientes de la función cuadrática a través de los
deslizadores 
y 
2.
Observar como se modifican los puntos de intersección 
y 
(cuando los hay).
3.
Notar como se comporta el área.
4.
Particularmente verificar el comportamiento cuando la
parábola está por encima de la recta.
5.
Mover los coeficientes de la recta a través de los deslizadores
m y b.
6.
Observar como se modifican los puntos de intersección y (cuando los hay).
7.
Notar como se comporta el área.
8.
Activar la casilla de verificación del área bajo la parábola.
9.
Activar la casilla de verificación del área bajo la recta.
10. Activar la casilla de verificación del área
limitada entre las dos curvas.
11. Concluir que el signo del área de
intersección depende cual curva esté arriba con respecto a los puntos de
intersección.
12. Pulsar el icono que se sitúa arriba a la
derecha para regresar a la construcción inicial.