PLANTEAMIENTO
Se ilustra geométricamente la propiedad de reflexión de la parábola.
DEFINICIÓN
La parábola es el lugar geométrico de un punto en el plano que se mueve
de forma tal que equidista de una recta fija llamada directriz y de un punto
fijo llamado foco.
PROPIEDAD FOCAL DE LA PARÁBOLA
Un rayo paralelo al eje de la parábola y reflejado en ella pasa por el
foco.
Inversamente, un rayo de luz, que emane del foco, se refleja en la
parábola a lo largo de una trayectoria paralela al eje de la parábola, sin
importar cual sea el punto de reflexión.
Este hecho es útil en la construcción de linternas, faros automotrices y
faros buscadores, en los cuales el reflector tiene una sección transversal
parabólica y la fuente luminosa esta en el foco. Igualmente, en los telescopios
y receptores de radar, las señales de una fuente remota entran paralelas al eje
y se reflejan pasando por el foco, mediante un reflector parabólico. La potente
concentración que produce un reflector parabólico grande, como el de un
radiotelescopio, hace posible detectar y analizar señales luminosas muy
pequeñas.
El astrónomo holandés Willebrord Snell van Royen (1580-1626) descubrió que el ángulo del rayo
incidente (ángulo incidental) es igual al ángulo del rayo reflejado (ángulo de
reflexión), y eso sucede en los rayos luminosos reflejados en la superficie de
la parábola.
Geométricamente esto es:
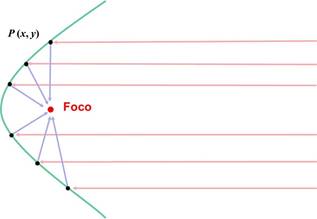
CONCLUSIÓN
La superficie generada al girar una parábola alrededor de su eje es una
superficie parabólica que refleja la energía emitida por un rayo y la concentra
en el foco. Un rayo de luz que procede del foco de la parábola se refleja en él
siguiendo una línea paralela al eje.
PROPUESTA
DE TRABAJO
1.
Identificar el foco de la parábola en color
rojo.
2.
Pulsar el botón de play
para ver la trayectoria de los rayos.
3.
Notar que cuando se emiten son de color verde y
una vez que chocan con la parábola se reflejan en color rosa y que todos
convergen en el foco.
4.
Regresar t a 0 e inmediatamente pausar la animación.
5.
Mover el deslizador n para fijar el número
de rayos y repetir el proceso.
6.
Regresar t a 0 e inmediatamente pausar la animación.
7.
La propiedad se cumple para cualquier parábola, mover el
parámetro p y comprobarlo.