PLANTEAMIENTO

Se expone el concepto de vector y las operaciones básicas entre dos vectores.

VECTOR

Un vector es un segmento de recta con dirección y sentido. Su representación gráfica consiste en una flecha, cuya punta va dirigida en dirección a la magnitud del estudio.

SUMA DE VECTORES

Para sumar dos vectores libres vector y vector se escogen como representantes dos vectores tales que el extremo de uno coincida con el origen del otro vector.

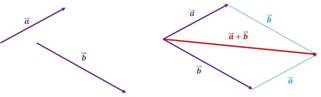
Método del paralelogramo: Dados dos vectores y ; si se aplica el método del paralelogramo para sumarlos, se debe considerar dos vectores iguales, a los dados, que se unen en su origen. Luego se dibuja un paralelogramo que tiene a ambos vectores como lados adyacentes, siendo la diagonal, del paralelogramo, la dirección del vector suma, cuyo origen coincide con el origen de los dos vectores. Gráficamente esto es:

RESTA DE VECTORES

Para restar dos vectores libres vector y vector se suma vector con el opuesto de vector.

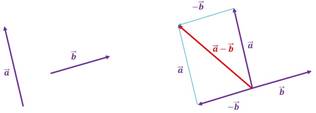
Para restar gráficamente un vector de un vector simplemente se suma con el opuesto a , es decir, .

PRODUCTO DE UN VECTOR POR UN ESCALAR

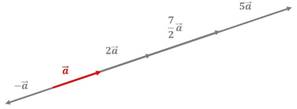
La multiplicación de un número por un vector es otro vector:

Con igual dirección que el vector .

Con el mismo sentido que el vector si .

Con sentido contrario del vector si .

De módulo

Ejemplo.

PROPUESTA DE TRABAJO

1. Identificar los vectores y .

2. Mover los deslizadores para modificar el módulo de los dos vectores.

3. Activar la casilla para ver la suma de los vectores.

4. Activar la casilla para ver la regla del paralelogramo.

5. Activar la casilla para ver la resta de los vectores.

6. Activar la casilla para ver vector en color café y desplazarlo. Notar como al hacerse más grande implica que se multiplica por un escalar mayor que uno, y al hacerse más pequeño, implica que se multiplica por un escalar menor que uno.

7. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.