PLANTEAMIENTO

Se ilustra geométricamente la ley de los senos.

LEY DE LOS SENOS

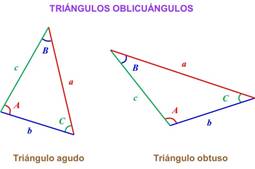
Un triángulo oblicuángulo es un triángulo que no es rectángulo. Puede ser un triángulo agudo (si sus tres ángulos son menores de 90°) o puede ser un triángulo obtuso (si uno de sus tres ángulos es mayor de 90°).

Por convención, se establece que los ángulos de un triángulo oblicuo son A, B, C y sus lados opuestos se identifican como a, b y c respectivamente. Esto se muestra en las siguientes figuras:

En cualquiera de los dos casos, la ley de los senos establece que:

Esta ley tiene tres igualdades y se puede usar en dos formas:

I) Si se conocen dos ángulos y el lado opuesto de ellos, se puede determinar el otro lado.

Ejemplo.

Si

Solución.

Aplicando la ley de los senos se tiene:

II) Si se conocen dos lados y el ángulo opuesto de uno de ellos, entonces también se puede determinar el ángulo opuesto del otro lado.

Ejemplo.

Si

Solución.

Aplicando la ley de los senos se tiene:

Nótese como puede no ser la única respuesta correcta, ya que hay dos ángulos entre 0° y 180° que tienen el mismo valor del seno (el segundo es el complemento del primero). Así que en este caso, otro resultado es el ángulo obtuso 180°-50.47° =129.52°.

Existen situaciones que son indeterminadas en que conociendo dos lados y el ángulo opuesto de uno de ellos, no siempre es suficiente para determinar el triángulo.

Ejemplo

Si

Solución.

Aplicando la ley de los senos se tiene:

No hay solución debido a que no es posible construir un triángulo con esos datos.

CONCLUSIÓN

Si dos lados y un ángulo opuesto a uno de ellos es dado, se pueden presentar tres posibilidades en la aplicación de la ley de los senos: que tenga solución única, que existan dos triángulos diferentes y que no exista el triángulo.

PROPUESTA DE TRABAJO

1. Recordar que un triángulo obtusángulo es un triángulo que no posee un ángulo recto.

2. Para ver la obtención del lado a y el ángulo A, activar la casilla correspondiente.

3. Activar la casilla correspondiente para ver la obtención del lado b y el ángulo B.

4. Para ver la obtención del lado c y el ángulo C, activar la casilla correspondiente.

5. Notar que los valores que se obtienen son iguales a los valores que se muestran en el triángulo.

6. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.

7. Mover el punto a la izquierda para establecer los valores , efectuar los cálculos correspondientes en el cuaderno para encontrar A, c y C y comprobarlos activando las casillas.