PLANTEAMIENTO

Se ilustra geométricamente el concepto de función logarítmica.

DEFINICIÓN DE LOGARÍTMO

Sea la expresión:

Se define al logaritmo en base a de un número b como el exponente n al que hay que elevar la base para obtener dicho número, esto es:

Que se lee: el logaritmo en base a del número b es n.

Ejemplos:

Como se puede ver, un logaritmo no es otra cosa que un exponente, hecho que no se debe olvidar cuando se trabaje con logaritmos.

Los logaritmos fueron introducidos en las Matemáticas con el propósito de facilitar, simplificar o incluso, hacer posible complicados cálculos numéricos. Utilizando logaritmos se puede convertir productos en sumas, cocientes en restas, potencias en productos y raíces en cocientes.

La constante a es un número real positivo distinto de uno, y se denomina base del sistema de logaritmos. La potencia para cualquier valor real de n sólo tiene sentido si .

Logaritmos decimales

Se llaman logaritmos decimales a los logaritmos que tienen por base el número 10. Al ser muy habituales es frecuente no escribir la base: El logaritmo decimal de potencias de diez (con números naturales) es el número de ceros que posee.

Logaritmos naturales

Se llaman logaritmos naturales (hiperbólicos o neperianos) a los logaritmos que tienen por base el número e:

el número e es un número irracional muy importante en Matemáticas y su valor es y se calcula mediante la expresión:

para cuando x es muy grande.

Cambio de base

Para hallar el logaritmo de un número en cualquier base, se puede efectuar aplicando la expresión:

Por conveniencia se utiliza generalmente la base b=10, así que la expresión anterior se convierte en:

Ejemplo.

Calcular el

Solución.

Antilogaritmo

Es el número que corresponde a un logaritmo dado. Consiste en el problema inverso al cálculo del logaritmo de un número.

Es decir, consiste en elevar la base al número resultado.

Del ejemplo anterior:

FUNCIÓN LOGARÍTMICA

Una función logarítmica con base a se define como:

La función logarítmica es biyectiva definida de R⁺ en R y sus características son:

· La función logarítmica solo está definida sobre los números positivos.

· Los números negativos y el cero no tienen logaritmo.

· La función logarítmica de base a es la recíproca de la función exponencial de base a.

· Las funciones logarítmicas más usuales son la de base 10 y la de base e.

· Es la función inversa de la función exponencial.

DOMINIO, RANGO Y GRÁFICA DE FUNCIONES LOGARÍTMICAS

· El dominio de la función logarítmica es el intervalo abierto: .

· El rango de la función logarítmica es el conjunto de todos los números reales positivos:

· No cruza al eje y, siempre corta al eje x en el punto y pasa por el punto .

· Siempre es creciente si y siempre es decreciente si .

· La función crece más lento si la base es cada vez mayor y decrece más lento si la base es cada vez menor.

· Es continua.

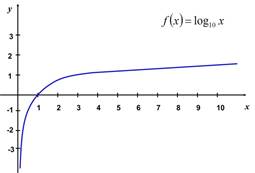
Ejemplo de la gráfica de la función cuando :

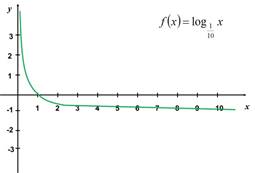
Ejemplo de la gráfica de la función cuando :

CONCLUSIÓN

Una función logarítmica es una función de la forma donde R con y x es un número real. Cuando , la función es creciente. Cuando , la función es decreciente.

PROPUESTA DE TRABAJO

1. Notar que la función es de la forma

2. Mover el deslizador hacia la derecha y observar que a medida que crece la base, la función crece más lento.

3. Ubicar el deslizador en y explicar que le sucede a la función.

4. Mover el deslizador hacia la izquierda y observar que a medida que decrece la base, la función decrece más lento.

5. Explicar por qué la base a no puede ser negativa ni cero

6. Observar que para todos los casos la función siempre es continua y pasa por el punto .

7. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.