PLANTEAMIENTO
Se ilustra geométricamente el concepto de función inversa.
FUNCIÓN INVERSA
Si f es una función que tiene por dominio al conjunto A y por rango al conjunto B , entonces se llama la
función inversa de f , aquella que tiene por dominio el conjunto B y por rango al conjunto A. A la función inversa de
f se le denota por ![]() Esquemáticamente esto es:
Esquemáticamente esto es:
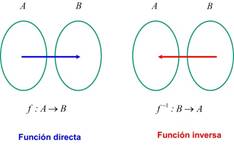
Dada una función ![]() , su inversa es otra función, designada por
, su inversa es otra función, designada por
![]() de
forma que se verifica que si
de
forma que se verifica que si ![]() , entonces
, entonces ![]()
Para encontrar la
regla de correspondencia de la función inversa, se debe despejar x de la función original ya que, para la función inversa, esa
es la variable dependiente. En otras palabras se efectúa el procedimiento siguiente:
-
Se define ![]()
-
Se intercambia x por y.
-
Se manipula algebraicamente para despejar y que es ![]() , es decir, la inversa de la función dada.
, es decir, la inversa de la función dada.
Es importante
recalcar que no todas las funciones tienen inversa, sólo aquellas que
son biyectivas.
Las gráficas de dos
funciones inversas son simétricas respecto de la bisectriz del primer cuadrante
y del tercer cuadrante.
Nota: ![]() no
significa
no
significa ![]()
Ejemplos.
Obtener la función inversa de las siguientes funciones:
1) ![]()
Solución.
Se establece: ![]()
Intercambiando las
variables: ![]()
Despejando y: ![]()
![]()
2) ![]()
Solución.
Se establece: ![]()
Intercambiando las
variables: ![]()
Despejando y: ![]()
![]()
Nótese como para
que cumpla con la definición de función, sólo se toma la raíz positiva.
3) ![]()
Solución.
Se establece: ![]()
Intercambiando las
variables: ![]()
Despejando y: ![]()
![]()
CONCLUSIÓN
Si la función ![]() está
definida por las parejas
está
definida por las parejas ![]() entonces la función inversa
entonces la función inversa ![]() es
la función definida por las parejas
es
la función definida por las parejas ![]() Esto
significa que el dominio de la función
Esto
significa que el dominio de la función ![]() es
el codominio de
es
el codominio de ![]() , y el codominio de la función
, y el codominio de la función ![]() es
el dominio de
es
el dominio de ![]() Esta
característica sólo la pueden cumplir las funciones biyectivas.
Esta
característica sólo la pueden cumplir las funciones biyectivas.
PROPUESTA
DE TRABAJO
1. Identificar que la función ![]() es
biyectiva (que es uno a uno y que su rango es igual al codominio).
es
biyectiva (que es uno a uno y que su rango es igual al codominio).
2. Mover el punto azul A sobre la función y ver el
comportamiento del punto rojo A’.
3. Concluir que los puntos de la
función ![]() son
son ![]() y
que los puntos de la función
y
que los puntos de la función ![]() son
son ![]() es
decir, se intercambian las parejas ordenadas.
es
decir, se intercambian las parejas ordenadas.
4.
Observar que las gráficas de dos funciones inversas son
simétricas respecto de la bisectriz del primer cuadrante y del tercer cuadrante
que se representa por la recta en verde.
5.
Comprobar que las gráficas corresponden al ejercicio 3.
6. Pulsar el icono que se sitúa
arriba a la derecha para regresar a la construcción inicial.