PLANTEAMIENTO
Se ilustra geométricamente el concepto de función exponencial.
FUNCIÓN EXPONENCIAL
Una función exponencial con base a se define como:
![]()
Donde ![]() R con
R con ![]() y x es un número real.
y x es un número real.
Esto significa que
la base de la función exponencial siempre es positiva, por lo que el valor de ![]() siempre es positivo. Además, la base no puede
ser la unidad, porque se convertiría en la función constante
siempre es positivo. Además, la base no puede
ser la unidad, porque se convertiría en la función constante ![]() .
.
Es importante que
esta función no se confunda con la función ![]() cuya base es x que asocia a cada número real a un
número positivo
cuya base es x que asocia a cada número real a un
número positivo ![]() . El comportamiento de estas funciones es
muy distinto. Para ejemplificar esto, se toma el valor de a = 3 y tabulando ambas funciones, se tiene:
. El comportamiento de estas funciones es
muy distinto. Para ejemplificar esto, se toma el valor de a = 3 y tabulando ambas funciones, se tiene:
|
|
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
-27 |
-8 |
-1 |
0 |
1 |
8 |
27 |
64 |
125 |
216 |
|
|
0.037 |
0.111 |
0.333 |
1 |
3 |
9 |
27 |
81 |
243 |
729 |
Como puede
apreciarse, la diferencia de valores es considerable, ya que en la primera
función sólo se calcula el cubo del número y en la segunda se comporta de forma
exponencial.
DOMINIO, RANGO Y GRÁFICA DE FUNCIONES
EXPONENCIALES
·
El dominio de la función exponencial es el
intervalo abierto: ![]()
·
El rango de la función exponencial es el
conjunto de todos los números reales positivos: ![]()
·
No cruza al eje x, siempre corta al eje y en el punto ![]() y pasa por el punto
y pasa por el punto ![]()
·
Siempre es creciente si ![]() y siempre es decreciente si
y siempre es decreciente si ![]()
·
La función crece más rápido si la base es cada
vez mayor y decrece más rápido si la base es cada vez menor.
·
Es continua.
·
Si el valor de la base es uno, a se convierte en la función constante ![]() ,
representada por una recta paralela al eje x,
a una unidad de distancia.
,
representada por una recta paralela al eje x,
a una unidad de distancia.
Ejemplo de la gráfica
de la función ![]() cuando
cuando ![]()
![]() :
:
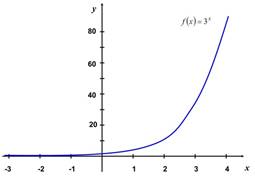
Ejemplo de la gráfica
de la función ![]() cuando
cuando ![]()
![]() :
:
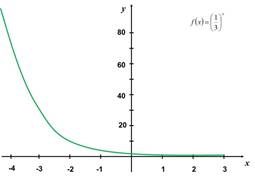
CONCLUSIÓN
Una función
exponencial es una función de la forma ![]() donde
donde
![]() R con
R con ![]() y x es un número real. Cuando
y x es un número real. Cuando ![]() , la función es creciente. Cuando
, la función es creciente. Cuando ![]() , la función es decreciente.
, la función es decreciente.
PROPUESTA
DE TRABAJO
1. Notar que la función es de la
forma ![]()
2. Mover el deslizador hacia la
derecha y observar que a medida que crece la base, la función crece más rápido.
3. Ubicar el deslizador en ![]() y
notar que la función resultante es la función constante
y
notar que la función resultante es la función constante ![]()
4. Mover el deslizador hacia la
izquierda y observar que a medida que decrece la base, la función decrece más
rápido.
5. Explicar por qué la base a no puede ser negativa ni cero![]()
6. Observar que para todos los casos
la función siempre es continua y pasa por el punto ![]() .
.
7. Pulsar el icono que se sitúa
arriba a la derecha para regresar a la construcción inicial.