PLANTEAMIENTO

Se expone la ecuación pendiente-ordenada al origen de la recta.

ECUACIÓN DE LA RECTA PENDIENTE-ORDENADA AL ORIGEN

Si en el caso de la ecuación punto-pendiente, el punto se desplaza hasta que coincida con el eje , se tiene:

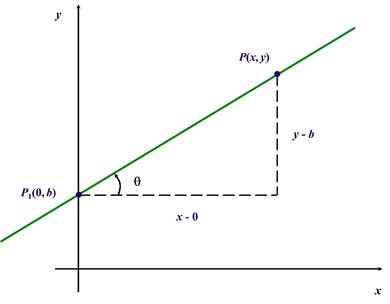
Se advierte que el punto se convierte en , donde es la ordenada al origen.

Para este caso la pendiente es:

ahora, si se despeja : , es decir:

que es la ecuación pendiente-ordenada al origen de la recta.

Ejemplos.

Determinar la ecuación de la recta dadas su pendiente y su ordenada al origen.

1) Pendiente y ordenada al origen

Solución.

2) Pendiente y con ordenada al origen

Solución.

CONCLUSIÓN

La ecuación pendiente-ordenada al origen de la recta se plantea si se conoce su pendiente y el punto en el que cruza al eje :

PROPUESTA DE TRABAJO

1. Modificar la pendiente en el deslizador y ver cómo se comporta la recta: cuando es positiva, cuando es negativa y cuando es cero.

2. Ver cómo cambia la ecuación en cada caso.

3. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.

4. Modificar el valor de la ordenada al origen y comprobar que es la distancia que hay del origen al cruce con el eje .

5. Ver cómo se comporta la recta y su ecuación.

6. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.

7. Comprobar los resultados de los dos ejemplos mostrados.

8. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.