PLANTEAMIENTO

Se expone la ecuación de la recta que pasa por dos puntos.

ECUACIÓN DE LA RECTA QUE PASA POR DOS PUNTOS

Dados los puntos , y de una recta:

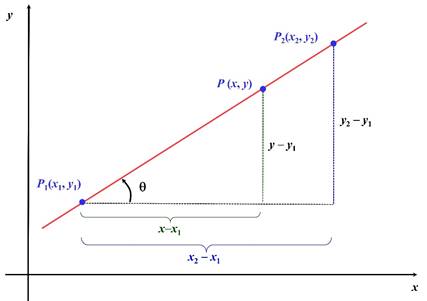
se observa que la pendiente que une a los puntos y es:

y que la pendiente que une a los puntos y es:

pero como la pendiente es la misma se pueden igualar:

que equivale a:

que es la ecuación conocida como de dos puntos o cartesiana de la recta.

Ejemplos.

Determinar la ecuación de la recta que pase por los puntos dados

1) y

Solución.

2) y

Solución.

CONCLUSIÓN

La ecuación de la recta cartesiana se usa si se conoce dos de sus puntos:

PROPUESTA DE TRABAJO

1. Modificar el punto , ver cómo se comporta la pendiente de la recta y su ecuación.

2. Modificar el punto , ver cómo se comporta la pendiente de la recta y su ecuación.

3. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.

4. Comprobar la equivalencia de los resultados de los dos ejemplos mostrados.

5. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.