PLANTEAMIENTO

 

Se ilustra geométricamente el concepto de ecuación general de segundo grado.

 

 

DEFINICIÓN DE CÓNICA

 

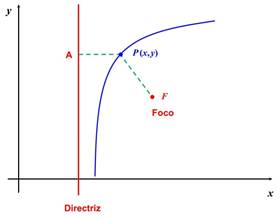
Dada una recta fija  L  y un punto fijo  F  no contenido en esa recta, se llama cónica al lugar geométrico de un punto  P  que se mueve en el plano, de tal manera que la razón de su distancia de F a su distancia de L es siempre igual a una constante positiva.

 

La recta L se llama directriz, el punto F, foco y la constante positiva, excentricidad de la cónica (e).

 

Gráficamente esto es:

 

 

 

 

Cuando e = 1, la definición anterior corresponde a una PARÁBOLA

Cuando e < 1, la definición anterior corresponde a una ELIPSE

Cuando e > 1, la definición anterior corresponde a una HIPÉRBOLA

 

 

ECUACIÓN GENERAL DE SEGUNDO GRADO

 

La ecuación general de segundo grado en dos variables se define como:

 

 

y puede representar una cónica del género parábola, elipse o hipérbola, según el indicador:

 

 

Según sea cero, negativo o positivo respectivamente.

 

Esto puede resumirse en la siguiente tabla:

 

ECUACIÓN GENERAL DE SEGUNDO GRADO:

 

Ax2+Bxy+Cy2+Dx+Ey+F=0

 

PARÁBOLA

ELIPSE

HIPÉRBOLA

INDICADOR

I = B2 - 4AC

I = 0

I < 0

I > 0

EXCENTRICIDAD

e

e = 1

e < 1

e > 1

 

 

TRASLACIÓN Y ROTACIÓN DE LOS EJES COORDENADOS 

 

Los ejes coordenados fueron concebidos como una herramienta que sirve para poder representar puntos y curvas en un plano. Sin embargo, existen lugares geométricos cuya naturaleza requiere de cambios en los ejes y se necesitan representar mediante una traslación, de una rotación o de una combinación de ambas.

 

En la ecuación general de segundo grado:

 

 

 

Los términos D y E determinan si está o no trasladada la cónica.

 

Una traslación implica que el lugar geométrico conserva su misma forma pero de forma paralela a los ejes coordenados, es decir, produce un nuevo conjunto de ejes paralelos a los originales. En ese sentido se cumple que:

 

-       Si  D ≠ 0  y  E ≠ 0  significa que está en cualquier punto del plano.

-       Si  D = 0  significa que está sobre el eje y.

-       Si  E = 0  significa que está sobre el eje x.

-       Si  D = E = 0  significa que está en el origen.

 

En una rotación, la forma del lugar geométrico no se altera, sin embargo, su posición respecto a los ejes coordenados no es paralela. Si en la ecuación general de segundo grado, se cumple que B ≠ 0, se tiene una rotación de los ejes x y y en donde su origen permanece fijo y ambos giran alrededor de éste un cierto ángulo.

 

En este sentido, el término Bxy implica que la cónica está rotada con respecto a los ejes coordenados. Considerando lo anterior, si B = 0, la cónica es paralela o coincidente a los ejes x y y.

 

 

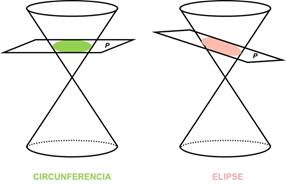
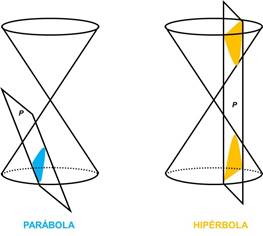
SECCIONES PLANAS DE UN CONO CIRCULAR RECTO

 

El nombre de secciones cónicas con que se designa a la parábola, elipse e hipérbola tiene su origen en el hecho de que estas curvas se obtuvieron por primera vez como secciones planas de un cono circular recto.

 

Gráficamente, los cortes de los conos son:

 

 

 

 

 

CONCLUSIÓN

 

La ecuación general de segundo grado es de la forma   y a través del indicador    puede determinarse si se trata de una elipse, una parábola o una hipérbola si respectivamente es menor, igual o mayor a cero.

 

 

PROPUESTA DE TRABAJO

 

1.      Moviendo el deslizador C hasta 3, comprobar que si A = C se tiene una circunferencia y que I < 0.

2.      Moviendo el deslizador C > 3, comprobar que si A ≠ C pero son del mismo signo, es una elipse y que I < 0.

3.      Moviendo el deslizador C < 0, comprobar que si A ≠ C y de signos distintos, es una hipérbola y que I > 0.

4.      Comprobar que si A ≠ 0, C = 0 y E ≠ 0, es una parábola que se abre hacia arriba o hacia abajo y que I = 0.

5.      Comprobar que si A = 0, C ≠ 0 y D ≠ 0, es una parábola que se abre hacia la derecha o a la izquierda y que I = 0.

6.      Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.

7.      Comprobar que si B ≠ 0 la curva tiene una rotación.

8.      Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.

9.      Comprobar que si D ≠ 0 la curva presenta un desplazamiento con respecto al eje x.

10.    Comprobar que si E ≠ 0 la curva presenta un desplazamiento con respecto al eje y.

11.    Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.