PLANTEAMIENTO

Se ilustra geométricamente como obtener una circunferencia y su ecuación a partir de conocer su centro y uno de sus puntos.

DEFINICIÓN

Una circunferencia se define como el lugar geométrico de los puntos que equidistan de un punto fijo en el plano llamado centro. La distancia que existe de cualquiera de sus puntos al centro recibe el nombre de radio.

OBTENCIÓN DEL RADIO Y ECUACIÓN

Al no tener el radio como dato debe encontrarse mediante la distancia que separa a los puntos. Esa distancia viene dada por:

Considerando a P como punto uno y al centro como punto dos. Geométricamente esto es:

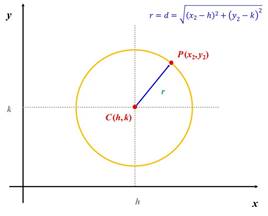
Una vez conocido el radio se aplica sustituye, junto con el centro, en la ecuación ordinaria y al desarrollarla se obtiene su ecuación general.

Ejemplo.

Obtener la ecuación de la circunferencia con centro en y que pase por el punto .

Sustituyendo las coordenadas de los puntos:

Sustituyendo el radio y el centro en la ecuación ordinaria, se tiene:

Para encontrar su ecuación general, se desarrollan los binomios, se acomoda y se simplifican los términos independientes:

CONCLUSIÓN

Para encontrar la ecuación de la circunferencia sólo se requiere del centro y el radio. Como en este caso no se tiene el radio, se requiere encontrarlo mediante la distancia que separa a los puntos dados.

PROPUESTA DE TRABAJO

1. Identificar el centro C en color rojo y el punto P también en color rojo que pertenece a la circunferencia.

2. Mover el centro y ver la ubicación de la circunferencia.

3. Mover el punto P para ver el comportamiento del radio.

4. Activar la casilla para observar el valor del radio.

5. Activar la casilla para visualizar las ecuaciones ordinarias y general de la circunferencia.

6. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.

7. Mover el centro y el punto y analizar el comportamiento de la ecuación.

8. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.