PLANTEAMIENTO

Se ilustra geométricamente como obtener una circunferencia y su ecuación a partir de conocer dos de sus puntos y una recta tangente a ella.

DEFINICIÓN

Una circunferencia se define como el lugar geométrico de los puntos que equidistan de un punto fijo en el plano llamado centro. La distancia que existe de cualquiera de sus puntos al centro recibe el nombre de radio.

PROCEDIMIENTO

Dados dos puntos A, B y una recta r, construir  la circunferencia que pase por los dos puntos y sea tangente a la recta.

El problema presenta tres casos posibles en función de la posición de A y B respecto a r:

CASO I. Los puntos A y B están situados en el mismo lado respecto de la recta r.

· Se traza la circunferencia con centro en M, que es el punto medio de A  y B.

· Se traza la recta que pasa por A y B que corta a la recta r en el punto C.

· Se construye la recta tangente a la circunferencia de centro en C. El punto de tangencia es D.

· La circunferencia con centro en C que pasa por D determina en r los puntos Q y R, puntos de tangencia.

· Las el centro de la circunferencia que pasa por A, B y Q, es el punto de intersección de la mediatriz del segmento AB y la perpendicular a r que pasa por Q. Similarmente, el centro de la circunferencia que pasa por A, B y R es el punto de intersección de la mediatriz del segmento AB y la perpendicular a r que pasa por R.

Gráficamente esto es:

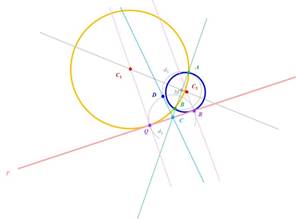
CASO II. La recta que pasa por A y B es paralela a la recta r.

· Basta con trazar la mediatriz de AB, que corta a r en el punto P, que es el punto de tangencia y se traza la circunferencia que pasa por A, B y P. La solución es única.

Gráficamente esto es:

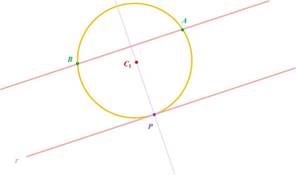
CASO III. Si A y B, están uno a cada lado de la recta

· El problema no tiene solución.

Gráficamente esto es:

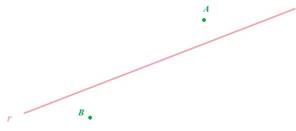
CONCLUSIÓN

Para encontrar la circunferencia a partir de conocer dos de sus puntos y una recta tangente a ella depende de la posición relativa de los puntos A y B respecto a la recta r.

PROPUESTA DE TRABAJO

1. Para visualizar el caso I, activar el botón reproduce y observar la construcción.

2. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.

3. Para visualizar el caso I paso a paso, pulsar reiteradamente el tercer botón.

4. Mover el punto a , el punto a , el punto a y el punto hasta . Apreciar que la recta AB y la recta r son paralelas porque sus pendientes valen 2. Mover el punto cerca de hasta nuevamente situarlo ahí y notar que los datos de la circunferencia café son muy grandes hasta que desaparece. Por su parte ver que los puntos D y tienden a unirse. Notar que la circunferencia azul desaparece debido a la construcción, sin embargo existe, y es la que pasa por los puntos A, B y R.

5. Mover el punto hasta y notar que los puntos A y B están en lados opuestos a la recta r. Analizar lo que sucede.

6. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.

7. Reproducir la animación una vez terminada, efectuar analíticamente en el cuaderno todo el proceso de obtención de ecuaciones las dos circunferencias y comprobar los resultados.

8. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.