PLANTEAMIENTO

Se ilustra geométricamente el área de un triángulo.

ÁREA DE UN TRIÁNGULO

Dados tres puntos , y no colineales en el plano, se genera un triángulo cuyos lados se forman al unir cada punto con los otros dos:

Gráficamente, es:

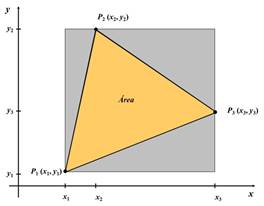
En la figura, el área del triángulo viene dada por el área del rectángulo menos el área de los tres triángulos sombreados, esto es:

Factorizando y :

Como el área no puede ser negativa, entonces:

Por otra parte, si se calcula el determinante dispuesto como se obtiene:

Obteniendo el mismo resultado, por lo tanto, el área de un triángulo también puede calcularse por:

Ejemplo.

Dados los puntos , y que son los vértices del triángulo, obtener su área mediante los dos procedimientos.

Solución.

CONCLUSIÓN

A través de la aplicación de la fórmula o del determinante, se puede encontrar el área de un triángulo dados sus vértices. El resultado siempre debe ser positivo.

PROPUESTA DE TRABAJO

1. Observar que los puntos mostrados determinan los vértices del triángulo.

2. Activar la casilla para ver su área.

3. Mover los puntos para ver como se transforma el triángulo y su área.

4. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.

5. Ubicar el punto en . Explicar lo que sucede.

6. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.

7. Efectuar en el cuaderno la obtención del área con los puntos dados, aplicando la fórmula. Comprobar el resultado obtenido con el mostrado.