PLANTEAMIENTO

Se ilustra geométricamente el ángulo entre dos rectas.

ÁNGULO ENTRE DOS RECTAS

Sean dos rectas y con sus respectivas pendientes y :

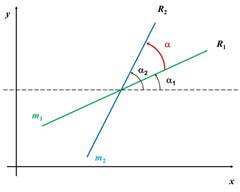
Se aprecia que:

La tangente del ángulo de intersección es:

Aplicando la identidad trigonométrica:

Y como y , se tiene que:

Por lo tanto, el ángulo de intersección de dos rectas y está dado por la expresión:

Si el resultado es mayor de 90°, el ángulo menor se obtiene restando el resultado a 180°.

Ejemplo.

Determinar el ángulo de intersección de entre las rectas:

y

Solución.

Para

Para

Sustituyendo se tiene:

CONCLUSIÓN

Se llama ángulo de dos rectas al menor de los ángulos que forman éstas. El ángulo se mide desde hasta .

PROPUESTA DE TRABAJO

1. Observar que los deslizadores determinan los coeficientes de las rectas en su forma general.

2. Activar la casilla para ver las ecuaciones de las rectas.

3. Activar la casilla para ver el ángulo de intersección entre ellas.

4. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.

5. Sin mover la recta , modificar los deslizadores de para fijar la recta en y observar el valor del ángulo. Explicar que característica poseen esas rectas.

6. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.

7. Sin mover la recta , modificar los deslizadores de para fijar la recta en y observar el valor del ángulo. Explicar que característica poseen esas rectas.

8. Pulsar el icono que se sitúa arriba a la derecha para regresar a la construcción inicial.

9. Efectuar en el cuaderno el proceso de obtención ángulo con los datos dados. Comprobar el resultado obtenido con el mostrado.