PLANTEAMIENTO
Se expone la solución de un sistema de dos inecuaciones con dos
incógnitas.
SISTEMA DE DOS INECUACIONES CON DOS
INCÓGNITAS.
Un sistema de dos inecuaciones lineales
con incógnitas 
y 
, es de la
forma:
o cualquier otro signo
de desigualdad, donde 
son coeficientes reales y 
son términos independientes. En cada una de
las inecuaciones, por lo menos uno de los coeficientes de las incógnitas es
diferente de cero. Resolver un sistema
de este tipo es obtener el semiplano solución de las dos desigualdades e
identificar su intersección.
Obtener la solución de
un sistema de este tipo supone obtener el hiperplano solución de cada una de
las inecuaciones que lo forman y determinar la intersección de todos ellos.
La solución de un
sistema de 
inecuaciones lineales con dos incógnitas es
siempre un conjunto convexo. Se llama
conjunto convexo a una región del plano tal que para dos puntos cualesquiera de
la misma, el segmento que los une está íntegramente contenido en dicha región.
Como casos particulares, un conjunto convexo puede quedar reducido a una recta,
a una semirrecta, a un segmento, a un punto o al conjunto vacío.
Los segmentos que
delimitan un conjunto convexo se llaman bordes o lados y, la intersección de
ellos, vértices. Los vértices y puntos de los lados que pertenezcan a la
solución del sistema de inecuaciones se denominan puntos extremos. Un conjunto
convexo puede ser cerrado o abierto respecto a cada lado o vértice según se
incluya éste o no en la solución. Puede ser acotado o no acotado según su área
sea o no finita.
Ejemplos.
Resolver los siguientes
sistemas de dos inecuaciones lineales con dos incógnitas.
1) 
Solución.
Convirtiendo a igualdad
la primera inecuación: 
Si 
Si 
la recta pasa por los
puntos 
y 
Para representar
gráficamente la solución de la primera inecuación se elige un punto que no esté
en la recta y se comprueba si verifica o no la desigualdad. Por ejemplo,
tomando el punto 
se aprecia que cumple la inecuación ya que al
sustituir se obtiene 
. Esto
significa que la región que incluye a ese punto es solución de esta
desigualdad.
Convirtiendo a igualdad
la segunda inecuación: 
Si 
Si 
la recta pasa por los
puntos 
y 
Para representar
gráficamente la solución de la segunda inecuación se elige un punto que no esté
en la recta y se comprueba si verifica o no la desigualdad. Por ejemplo,
tomando el punto 
se observa que cumple la inecuación ya que al
sustituir se obtiene 
. Esto
significa que la región que incluye a ese punto es solución de esta
desigualdad.
El conjunto solución es
la intersección de las dos regiones, formando el semiplano sombreado.
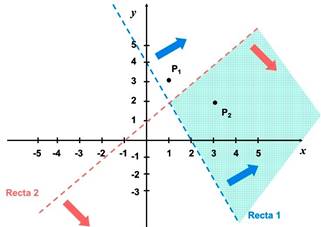
2) 
Solución.
Acomodando:
Convirtiendo a igualdad
la primera inecuación: 
Si 
Si 
la recta pasa por los
puntos 
y 
Se elige un punto que
no esté en la recta para verificar si cumple o no la desigualdad. Por ejemplo,
tomando al punto 
se tiene que 
, esto es,
cumple la inecuación, por lo que la región que incluye a ese punto es solución
de esta desigualdad.
Convirtiendo a igualdad
la segunda inecuación: 
Si 
Si 
la recta pasa por los
puntos 
y 
Se elige un punto que
no esté en la recta para verificar si cumple o no la desigualdad. Por ejemplo,
tomando al punto 
se tiene que
, esto es,
no cumple la inecuación, por lo que la región que no incluye a ese punto es
solución de esta desigualdad.
El conjunto solución es
la intersección de las dos regiones, formando el semiplano sombreado.
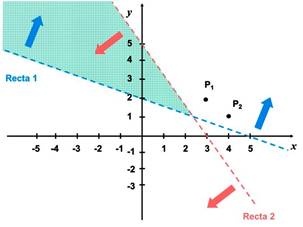
CONCLUSIÓN
La solución de un
sistema de inecuaciones es la intersección de las regiones que corresponden a
la solución de cada inecuación.
PROPUESTA
DE TRABAJO
1.
Ver los valores de los deslizadores en azul que son los que
determinan la primera inecuación.
2.
Ver los valores de los deslizadores en verde que son los que
determinan la segunda inecuación.
3.
Activar la casilla para ver la solución de la primera
inecuación. Desactivar la casilla.
4.
Activar la casilla para ver la solución de la segunda
inecuación.
5.
Volver a activar la casilla para ver la solución de la
primera inecuación.
6.
Concluir que la solución del sistema está dada por la intersección
de las regiones y está en color gris.
7.
Mover los deslizadores para establecer nuevas inecuaciones y
ver su conjunto solución.
8.
Pulsar el icono que se sitúa arriba a la derecha para
regresar a la construcción inicial.