PLANTEAMIENTO
Se ilustra cómo se puede obtener gráficamente la raíz cuadrada de un
número.
NÚMEROS IRRACIONALES
Con
los números racionales se pueden representar casi todas las cantidades que se
encuentran en la vida cotidiana. Sin embargo, hay otra clase de números, que se
escriben con una infinidad de decimales pero que no tienen un período, es
decir, no tienen cifras que se repitan en el mismo orden. Los números de esta
clase reciben el nombre de irracionales
y, a diferencia de los racionales, no pueden expresarse en forma de fracción,
sino sólo en forma decimal. Se denotan por Q’.
En
general, cualquier raíz inexacta de un número racional o alguna combinación
algebraica que la involucre (y que exista) es un número irracional. Este
conjunto también es infinito.
Ejemplos
de números irracionales:
TEOREMA DE LA ALTURA
Dada la figura:
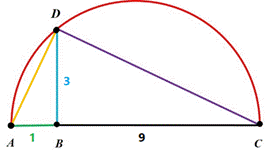
El teorema de la altura establece que el cuadrado de la altura sobre la hipotenusa de un triángulo rectángulo es
igual al producto de las proyecciones de sus catetos sobre la hipotenusa. Es decir que 
. Esto significa
que la altura es la media proporcional de las proyecciones, esto es:
que equivale a:
Entonces, se puede afirmar que el
segmento 
es la media proporcional (o geométrica) de los segmentos 
y 
.
Ahora, si el segmento 
, entonces
se cumple que:
CÁLCULO DE RAÍCES CUADRADAS
De acuerdo con lo anterior, se puede obtener la raíz cuadrada del
segmento conociendo la distancia .
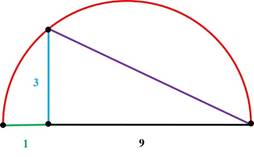
Por ejemplo, para conocer la raíz cuadrada de 
, basta
con sólo establecer el segmento marcado en negro en y visualizar el segmento en azul que
representa su raíz cuadrada, que es 
.
CONCLUSIÓN
Un número irracional, es aquel que no
se puede poner como cociente de dos números enteros.
La necesidad de los números
irracionales surge de medir longitudes sobre algunas figuras geométricas, por
ejemplo: la longitud de la diagonal de un cuadrado tomando como unidad el lado
del mismo es 
PROPUESTA
DE TRABAJO
1.
Mover
el punto 
que es el número al que se quiera extraer raíz
cuadrada.
2.
Pulsar el icono que
dice Triángulos.
3.
Analizar el teorema
de la altura.
4.
Notar que el
segmento se
fijó en 
para
simplificar el cálculo.
5.
Deducir que la
altura marcada en azul es justamente la raíz del
número buscado.
6.
Mover
el punto varias veces, observar su raíz cuadrada y
notar que los decimales mostrados son sólo un aproximado porque en realidad el
resultado tiene decimales infinitos que no se repiten.
7.
Pulsar el icono que
se sitúa arriba a la derecha para regresar a la construcción inicial.