PLANTEAMIENTO
Se exponen tres medidas de dispersión muy utilizadas para datos no
agrupados.
RANGO, DESVIACIÓN
ESTÁNDAR Y VARIANZA
El rango de una variable estadística se define como la diferencia entre
el mayor y el menor valor de la variable.
![]()
El rango indica la longitud del intervalo en el que se hallan todos los
datos de la distribución. El rango es una medida de dispersión importante,
aunque insuficiente para valorar convenientemente la variabilidad de los datos.
Ejemplo.
Calcular el rango de las
siguientes edades (en años) de alumnos del grupo 470-A de la prepa 8 de la UNAM
que son de excelencia académica: ![]() y
y ![]() .
.
Solución.
El valor mínimo es 14 años y el valor máximo es 18, por lo tanto:
![]()
DESVIACIÓN ESTÁNDAR
La desviación estándar es la
medida de dispersión más común, que indica qué tan dispersos están los datos
con respecto a la media. Mientras mayor sea la desviación estándar, mayor será
la dispersión de los datos. Se denota por medio de s.
Una desviación estándar grande
indica que los puntos están lejos de la media, y una desviación pequeña indica
que los datos están agrupados cerca de la media.
La fórmula para calcular la
desviación estándar es:
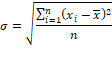
Ejemplo.
Calcular la desviación estándar
de las siguientes puntuaciones de un jugador de baloncesto de la UNAM en los
últimos partidos: ![]() y
y ![]() .
.
Solución.
Calculando la media aritmética:
![]()
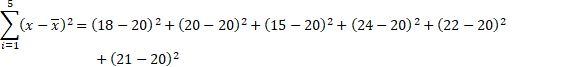
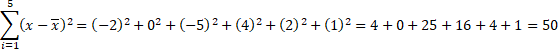
![]()
La interpretación es
que el jugador es muy constante ya que su desviación estándar es pequeña en
comparación de la media, debido a que tiene puntuaciones muy similares.
VARIANZA
Está considerada, junto con la
desviación estándar, el mejor indicador de la variabilidad global de la
distribución. Mide la dispersión de los datos respecto a la media aritmética,
de hecho, suministra el valor medio del cuadrado de las desviaciones de los
valores respecto de la media:
La varianza mide la mayor o menor
dispersión de los valores de la variable respecto a la media aritmética. Cuanto
mayor sea la varianza mayor dispersión existirá y por tanto, menor representatividad
tendrá la media aritmética. La varianza se expresa en las mismas unidades que
la variable analizada, pero elevadas al cuadrado.
Se denota por n y su expresión es:
![]()
Nótese como la varianza es igual
al cuadrado de la desviación estándar.
Ejemplo.
Las edades de los pacientes de un
doctor en un día fueron las siguientes: ![]() y
y ![]() . Obtener la
varianza de las edades e interpretarla.
. Obtener la
varianza de las edades e interpretarla.
Solución.
Calculando la media aritmética:
![]()
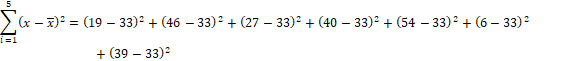
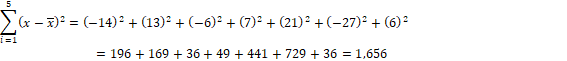
![]()
Este valor se
interpreta como que la media de las diferencias cuadráticas de los siete datos
con respecto a su media aritmética es alta, esto significa que las edades son
muy dispersas.
CONCLUSIÓN
Las
medidas de dispersión pueden definirse como los valores numéricos cuyo objeto
es analizar el grado de separación de los valores de una serie estadística con
respecto a las medidas de tendencia central consideradas.
PROPUESTA
DE TRABAJO
1.
En la tabla de la izquierda del applet se muestran las calificaciones
de un grupo cinco alumnos de una clase de estadística avanzada.
2.
Comprobar en el cuaderno el cálculo del rango.
3.
Corroborar en el cuaderno el cálculo de la media aritmética.
4.
Comprobar en el cuaderno el cálculo de la suma de
desviaciones al cuadrado.
5.
Corroborar en el cuaderno el cálculo de la varianza.
6.
Comprobar en el cuaderno cálculo de la desviación estándar y
establecer su interpretación.
7.
Cambiar los datos de las calificaciones y repetir el proceso.
8.
Pulsar el icono que se sitúa arriba a la derecha para
regresar a la construcción inicial.