PLANTEAMIENTO
Se expone la aplicación del triángulo de Pascal en el desarrollo del binomio
de Newton.
BINOMIO
DE NEWTON
El teorema del binomio, también llamado binomio de Newton expresa la
enésima potencia de un binomio como un
polinomio. El desarrollo del binomio 
posee singular importancia ya que
aparece con mucha frecuencia en Matemáticas y posee diversas aplicaciones en
otras áreas del conocimiento.
Si el binomio de la forma 
se multiplica sucesivamente por sí mismo se
obtienen las siguientes potencias:
De los desarrollos anteriores, se observa que:
·
El desarrollo de 
tiene 
términos.
· El
exponente de 
empieza con 
en el primer término y va disminuyendo en uno
con cada término, hasta cero en el último.
· El
exponente de 
empieza con cero en
el primer término y va aumentando en uno con cada término, hasta en el
último.
· Para
cada término la suma de los exponentes de y es .
· El
coeficiente del primer término es uno y el del segundo es .
·
El coeficiente de un término cualquiera es igual al
producto del coeficiente del término anterior por el exponente de dividido entre el número que indica el orden
de ese término.
·
Los términos que equidistan de los extremos tienen
coeficientes iguales.
TRIÁNGULO
DE PASCAL
El triángulo de Pascal es un esquema que tiene
como característica que cada uno de los componentes de sus filas representa los
coeficientes del desarrollo binomial.
Se construye de la siguiente manera:
· Se empieza por el 
de la cumbre.
·
De
una fila a la siguiente se escriben los números con un desfase de medio lugar o
casilla para que cada casilla tenga dos números justo arriba, en la fila
anterior.
· Cada extremo de la fila
tiene un y el valor que se escribe en una casilla es la
suma de los números que están encima.
· Después,
se efectúa una relación entre los números del triángulo de Pascal y la suma de
las potencias de y ,
de forma que los coeficientes se asignan en el mismo orden en que aparecen.
Gráficamente esto es:
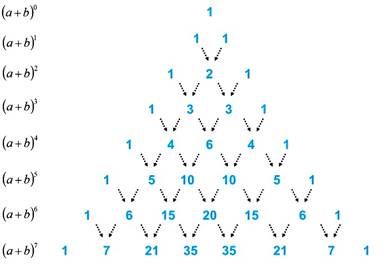
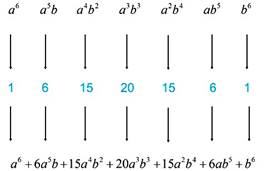
Por ejemplo, para encontrar los coeficientes
del desarrollo 
, se le aplican los
factores de la séptima fila, tal y como se muestra en la siguiente figura:
Ejemplos.
1) Aplicar el triángulo de Pascal para
desarrollar 
Solución.
Ubicando los coeficientes respectivos se tiene:
2) Encontrar la expansión de 
aplicando el triángulo de Pascal.
Solución.
Ubicando los coeficientes respectivos se tiene:
CONCLUSIÓN
El
triángulo de Pascal es un triángulo de números enteros, infinito y simétrico Se
empieza con un en la primera fila, y en las filas siguientes
se van colocando números de forma que cada uno de ellos sea la suma de los dos
números que tiene encima. La fórmula general del llamado Binomio de Newton está formada por los coeficientes que coinciden
con la línea número del triángulo de Pascal.
PROPUESTA
DE TRABAJO
1.
Mover el deslizador
para ver la construcción del triángulo de Pascal.
2.
Activar la casilla
para ver su respectiva expansión binomial.
3.
Ver el ejemplo
mostrado en azul y activar la casilla para ver su solución
4.
Pulsar el botón de
Nuevo para ver otro ejemplo.
5.
Concluir se pueden
usar las filas del triángulo de Pascal para facilitar el proceso de expansión
binomial ya representan a los coeficientes de los valores expandidos. Además,
concluir que se usa para
determinar la fila que se tiene que usar, en donde, representa a la potencia del binomio.
6.
Pulsar el icono que
se sitúa arriba a la derecha para regresar a la construcción inicial.