PLANTEAMIENTO
Se expone como obtener la recta por regresión lineal por el método de mínimos
cuadrados.
RECTA
DE REGRESIÓN LINEAL POR EL MÉTODO DE MÍNIMOS CUADRADOS
La
regresión lineal permite definir la
recta que mejor se ajusta a una nube de puntos. Gráficamente:
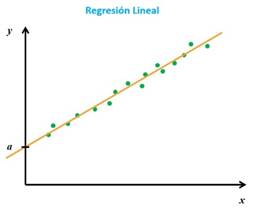
Este
método de regresión por mínimos cuadrados
es una estrategia adicional para ajustar adecuadamente el comportamiento o la
tendencia general de los datos a través de una recta que minimice la suma de
los cuadrados de las distancias verticales de los puntos a la recta.
Para
obtener una recta de la forma:
donde
es la variable dependiente y 
es la variable independiente. Sus coeficientes
representan:
Este
método se basa en la aplicación de las siguientes expresiones:
Ejemplo.
Aplicando
el método de mínimos cuadrados, obtener la recta de regresión para los
siguientes datos:
|
Estatura (m) |
1.72 |
1.79 |
1.78 |
1.75 |
1.80 |
1.79 |
1.81 |
1.70 |
1.68 |
1.73 |
|
Peso (kg) |
74 |
81 |
76 |
77 |
87 |
86 |
92 |
67 |
76 |
74 |
Solución.
Acomodando la tabla convenientemente y obteniendo 
y 
se tiene:
|
Estatura
|
Peso
|
|
|
|
1.72 |
74 |
127.28 |
2.9584 |
|
1.79 |
81 |
144.99 |
3.2041 |
|
1.78 |
76 |
135.28 |
3.1684 |
|
1.75 |
77 |
134.75 |
3.0625 |
|
1.8 |
87 |
156.6 |
3.24 |
|
1.79 |
86 |
153.94 |
3.2041 |
|
1.81 |
92 |
166.52 |
3.2761 |
|
1.7 |
67 |
113.9 |
2.89 |
|
1.68 |
76 |
127.68 |
2.8224 |
|
1.73 |
74 |
128.02 |
2.9929 |
|
17.55 |
790 |
1388.96 |
30.8189 |
Por lo que la recta de regresión lineal usando mínimos
cuadrados es: 
Su gráfica es:
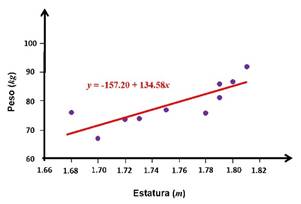
CONCLUSIÓN
La recta de regresión
es la que mejor se ajusta a la nube de puntos. La recta de regresión se utiliza
para estimar los valores de a partir de la 
El método de lo mínimos cuadrados es un
procedimiento de análisis numérico en la que, dados un conjunto de datos (pares
ordenados), se intenta determinar la función continua que mejor se aproxime a
los datos (línea de regresión o la línea de mejor ajuste), proporcionando una
demostración visual de la relación entre los puntos de los mismos. En su forma
más simple, busca minimizar la suma de cuadrados de las diferencias ordenadas
(llamadas residuos) entre los puntos generados por la función y los
correspondientes datos.
PROPUESTA
DE TRABAJO
1.
Observar detenidamente la tabla de datos
2.
Notar que esos datos están graficados en forma
de puntos.
3.
Mover el deslizador y ver cómo se genera la
recta.
4.
Activar la casilla para ver la recta y la ecuación
de regresión lineal.
5.
Notar la recta se ajusta lo más posible a la
nube de puntos
6.
Con los datos presentados, comprobar en el cuaderno la
ecuación de la recta siguiendo la metodología expuesta.
7.
Para modificar los puntos, usar el teclado que se ubica en el
extremo izquierdo.
8.
Pulsar el icono que se sitúa arriba a la derecha para
regresar a la construcción inicial.