PLANTEAMIENTO
Se exponen los conceptos de histograma, polígono de frecuencias y las
medidas de tendencia central.
HISTOGRAMA
Un histograma está compuesto por rectángulos, cuyo número
coincide con la cantidad de intervalos considerados, el ancho de la base de
cada uno de esos rectángulos es la misma siempre. Se emplea cuando la variable
independiente es categórica. Cada barra sólida, ya sea vertical u horizontal
representa un tipo de dato. Cuando es necesario representar divisiones de datos
se utiliza un gráfica de barras subdivididas. Los histogramas no muestran
frecuencias acumuladas, son preferibles para el tratamiento de datos
cuantitativos y la barra con mayor altura representa la mayor frecuencia. La
sumatoria de las alturas de las columnas equivale al 100% de los datos.
POLÍGONO DE FRECUENCIAS
Un polígono de frecuencia es el nombre que tiene el tipo de
gráfica que se realiza a partir de un histograma de frecuencia, en los cuales
se utilizan columnas verticales para expresar las frecuencias, el polígono se
crea al unir los puntos de máxima altura dentro de estas columnas.
MEDIDAS DE TENDENCIA
CENTRAL
Las medidas de tendencia central son medidas estadísticas
que se usan para describir cómo se puede resumir la localización de los datos.
Ubican e identifican el punto alrededor del cual se centra la información.
Estas medidas indican hacia donde se inclinan o se agrupan más los datos. Las
tres más importantes para datos agrupados son:
MEDIA
Si en una tabla de
distribución de frecuencia, con 
clases, los puntos medios son: 
y las respectivas frecuencias son 
, la media
aritmética se calcula de la siguiente manera:
Donde el número total
de observaciones es: 
MEDIANA
Cuando los datos se
encuentran agrupados en una distribución de frecuencia no se conocen los datos
originales, por lo tanto es necesario estimar la mediana 
mediante los siguientes pasos:
1. Calcular el valor 
2. Localizar el
intervalo de clase donde se encuentra la mediana (intervalo mediano). Esto se
hace encontrando el primer intervalo de clase donde la frecuencia acumulada es
igual o mayor que 
3. Aplicando la
siguiente fórmula con los valores del intervalo mediano:
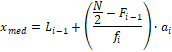
donde:
= Límite inferior de la clase de donde se
encuentra la mediana
= Total de
frecuencias
= Frecuencia
acumulada anterior a la clase mediana
= Frecuencia del intervalo mediano
= Amplitud del intervalo de clase
MODA
Es el valor que
representa la mayor frecuencia
absoluta. En tablas de frecuencias con datos agrupados, se habla de intervalo
modal.
Si todos los intervalos
tienen la misma amplitud, la moda 
se calcula por medio de:
donde:
= Extremo inferior del
intervalo modal (intervalo que tiene mayor frecuencia absoluta).
= Frecuencia absoluta
del intervalo modal.
= Frecuencia absoluta
del intervalo anterior al modal.
= Frecuencia absoluta
del intervalo posterior al modal.
= Amplitud de los
intervalos.
CONCLUSIÓN
Un histograma es una
representación gráfica de una variable en forma de barras, donde la superficie
de cada barra es proporcional a la frecuencia de los valores representados. Un
polígono de frecuencias se crea a partir de un histograma de frecuencia y se
obtiene uniendo los puntos de mayor altura de estas columnas. Las medidas de
tendencia central, son medidas estadísticas que pretenden resumir en un solo
valor a un conjunto de valores. Representan un centro en torno al cual se
encuentra ubicado el conjunto de los datos. Las medidas de tendencia central
más utilizadas son: media, mediana y moda.
PROPUESTA
DE TRABAJO
1.
Observar las frecuencias de los datos.
2.
Activar la casilla para ver las frecuencias.
3.
Activar la casilla para ver los intervalos.
4.
Activar la casilla para ver el polígono de
frecuencias.
5.
Activar la casilla de medidas para ver la
media, mediana y moda de los datos.
6.
Interpretar el significado de estas medidas y
su correspondencia con el histograma y polígono de frecuencias.
7.
Pulsar el icono que se sitúa arriba a la derecha para
regresar a la construcción inicial.